Question

As shown in figure, two poles of height 8m and 4m are perpendicular to the ground. If the length of shadow of a smaller pole due to sunlight is 6m then how long will be the shadow of the bigger pole at the same time?

Answer 1

Hint: Two given triangles seem to be similar according to AA similarity. According to which if two angles are equal then the triangle will be similar. Here we can see that $\angle R = \angle C = {90^ \circ }$and $\angle Q = \angle B$as the shadow at the same time so the angle of depression is the same. Then the two triangles $\Delta PQR \sim \Delta ABC$ then we will equate the ratio of corresponding sides and get the values of $x$ .

Complete step-by-step answer:

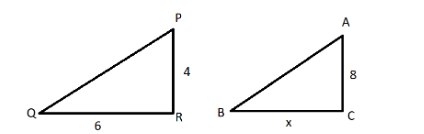
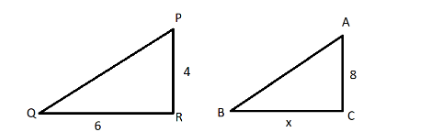
Given length of the pole $AC = 8m$ and formed the shadow of length of $BC = x$ which form a triangle $\Delta ABC$ and
The length of the pole $PR = 4m$ and formed the shadow of length of $RQ = 6m$ which form a triangle $\Delta PRQ$
Now in triangle $\Delta ABC$ and $\Delta PRQ$
Pole and shadow are perpendicular to each other
$\angle C = \angle R = {90^ \circ }$
As we are measuring the shadow of poles at same time so the angle of depression will be equal
$\angle B = \angle Q$
So, $\Delta PQR \sim \Delta ABC$ by AA similarity
Now, we can say that the ratio of corresponding sides is equal
$\dfrac{{PQ}}{{AB}} = \dfrac{{QR}}{{BC}} = \dfrac{{PR}}{{AC}}$
$\dfrac{{PR}}{{AC}} = \dfrac{{QR}}{{BC}}$
Now substituting the value of PR= 4m, QR= 6m, AB=8m and BC=x we get

$\Rightarrow$ $\dfrac{4}{8} = \dfrac{6}{x}$
On solving we will get the value of $x$
$\Rightarrow$ $x = 12m$

Note: Similar triangles: triangles are said to be similar if angles and ratio of corresponding sides are equal.

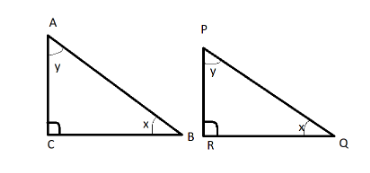
This triangle is said be similar if
$
  \angle A = \angle P \\
  \angle C = \angle R \\
  \angle B = \angle Q \\
 $
And $\dfrac{{PQ}}{{AB}} = \dfrac{{QR}}{{BC}} = \dfrac{{PR}}{{AC}}$