Question

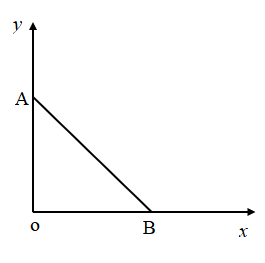
As per diagram, a charge q is placed at the origin O. Work done by a charge \[ - Q\] in taking it from \[{\text{A}}\left( {0,a} \right)\] to \[{\text{B}}\left( {a,0} \right)\] along the path AB:

A. Zero
B. \[\sqrt 2 a\left( {\dfrac{{qQ}}{{4\pi {\varepsilon _0}{a^2}}}} \right)\]
C. \[\left( {\dfrac{{ - qQ}}{{4\pi {\varepsilon _0}{a^2}}}} \right)\sqrt 2 a\]
D. \[\left( {\dfrac{{qQ}}{{4\pi {\varepsilon _0}{a^2}}}} \right)\dfrac{a}{{\sqrt 2 }}\]

Answer 1

Hint: We know that the work done is equal to change in potential energy. Calculate the potential energy of the system at position A and B simultaneously and take the difference of them to calculate the work done.

Complete step by step answer:
The potential energy of system of two point charges,
\[U = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q_1}{q_2}}}{r}\]
Here, \[{\varepsilon _0}\] is the permittivity of the free space, \[{q_1}\] and \[{q_2}\] are the two point charges and r is the separation between the point charges.

We know that the formula for potential energy of two point charges \[{q_1}\] and \[{q_2}\] separated by distance r is,
\[U = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q_1}{q_2}}}{r}\]
Here, \[{\varepsilon _0}\] is the permittivity of the free space.
We know, the work done to move the charge from one position to another is equal to the change in potential energy. Therefore, we have to calculate the potential energy of the two charges q and \[ - Q\] at position A and B.
The potential energy of the charges q and \[ - Q\] at position A is,
\[{U_A} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{q\left( { - Q} \right)}}{a}\]
\[ \Rightarrow {U_A} = - \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{qQ}}{a}\] …… (1)
Here is the distance of separation between two point charges.
The potential energy of the charges q and \[ - Q\] at position B is,
\[{U_B} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{q\left( { - Q} \right)}}{a}\]
\[ \Rightarrow {U_B} = - \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{qQ}}{a}\] …… (2)
Subtract equation (1) from equation (2).
\[{U_B} - {U_A} = \left( { - \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{qQ}}{a}} \right) - \left( { - \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{qQ}}{a}} \right)\]
\[ \Rightarrow {U_B} - {U_A} = 0\]
Therefore, the work done by the charge \[ - Q\] is,
\[W = {U_B} - {U_A}\]
\[ \Rightarrow W = 0\].

So, the correct answer is “Option A”.

Note:
In the formula, \[U = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q_1}{q_2}}}{r}\], r is the displacement of the point charge which should be taken as \[{r_2} - {r_1}\], where \[{r_2}\] is the final position and \[{r_1}\] is the initial position. In this question, \[{r_1}\] is at origin, therefore, we have neglected the term. The work done by the charge \[ - Q\] is always zero, as long as the distance between the charge q and \[ - Q\] does not change.