Question

As observed from the top of a lighthouse 100m high from sea-level, the angle of depression of two ships are ${{30}^{\circ }},{{45}^{\circ }}$ . If the ship is exactly behind the other on the same side of the light house, find the distance between the two ships (use $\sqrt{3}=1.732$ )
a) 60m
b) 73.2m
c) 75.32
d) 78.6

Answer 1

Hint: Angle of depression i.e. ${{30}^{\circ }},{{45}^{\circ }}$ will from the top with the horizontal line, corresponding angles by a transversal will be equal use this concept to get the required angles in the diagram. Apply tan trigonometric function with the two right angled triangles formed in the diagram. $\tan \theta $ in a right angle is given as
$\tan \theta =\dfrac{\text{Perpendicular}}{\text{Base}}$
And use:
\[\begin{align}
  & \tan {{45}^{\circ }}=1 \\
 & \tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}} \\
\end{align}\]

Complete step-by-step answer:
Let us collect the information provided in the problem as
i) Lighthouse is 100m from sea level.
ii) Angles of depression of two ships from top of lighthouse are ${{30}^{\circ }},{{45}^{\circ }}$
iii) Ships are on the same side of the light house.
Hence, we need to determine the distance between the ships with the help of above information. So, we can draw a diagram using the above details as

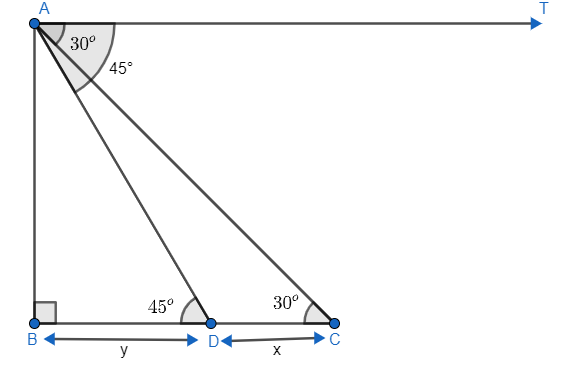
Where A is representing the top of the lighthouse and D and C are the points for representing ships. AB and CD are the lengths of the lighthouse and distance between ships respectively ${{30}^{\circ }},{{45}^{\circ }}$ are angles of depression for both the ships. And line AT and line through BC are parallel to each other as per the symmetry of the diagram. Hence, $\angle ACB,\angle ADB\Rightarrow {{30}^{\circ }},{{45}^{\circ }}$ respectively as AC and AD are acting as transversals between BC and AT and angles $\angle TAC,\angle ACB$ are representing corresponding angles between two parallel lines. So, as we know corresponding angles are equal hence we get
$\angle TAC=\angle ACB={{30}^{\circ }}$
Similarly we get
$\angle TAD=\angle ADB={{45}^{\circ }}$
So, in $\Delta ABD$ we can write
AB = 100m
BD = ym
As we know $\tan \theta $ for a right angle triangle can be defined as
$\tan \theta =\dfrac{\text{Perpendicular}}{\text{Base}}.............................\left( i \right)$
Hence, we get
$\tan {{45}^{\circ }}=\dfrac{100}{y}$
We know the value of $\tan {{45}^{\circ }}$ is 1. So, we get
$1=\dfrac{100}{y}$
y = 100 m…………………………(ii)
Similarly in triangle ABC we get
$\begin{align}
  & \tan {{30}^{\circ }}=\dfrac{AB}{BC} \\
 & \tan {{30}^{\circ }}=\dfrac{100}{x+y} \\
\end{align}$
We know the value of $\tan {{30}^{\circ }}\to \dfrac{1}{\sqrt{3}}$ . So, we get
$\begin{align}
  & \dfrac{1}{\sqrt{3}}=\dfrac{100}{x+y} \\
 & \Rightarrow \left( x+y \right)=100\sqrt{3} \\
\end{align}$
Putting value of y as 100 from the equation (i) we get
$x+100=100\sqrt{3}$
As it is given that $\sqrt{3}=1.732$ . So, we can get value of ‘x’ as
$\begin{align}
  & x=100\left( \sqrt{3}-1 \right) \\
 & x=100\left( 1.732-1 \right) \\
 & x=100\left( 0..732 \right) \\
 & x=73.2m \\
\end{align}$
Hence, the distance between both the ships is 73.2m. So, option (b) is correct.
Note: Diagram is the key point of the problem. One may go wrong if he or she represented the diagram as

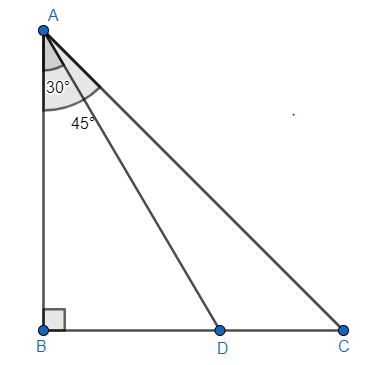
Where ${{30}^{\circ }},{{45}^{\circ }}$ are drawn with the vertical line AB, which is wrong. Angle of depression is defined with the horizontal line not with the vertical line. So, be clear with the problem perfectly.
One may use any other trigonometric functions such as $\sin ,\cos ,\sec ,cosec$ with both the triangles but we will get the required answer only using tan and cot functions. So, take care of this part in the problem as well.