Question

As observed from the top of a $80\text{ }m$ tall lighthouse, the angle of depression of two ships on the same side of the lighthouse in horizontal line with its base is $40{}^\circ \And 30{}^\circ $ respectively. Find the distance between two ships. Give your answer correct the nearest metre?

Answer 1

Hint: We apply trigonometry height and distance formula. In which we use either $\tan \theta \text{, }$ $\text{sin}\theta \text{ or cos}\theta \text{ }$ opposite to $\theta $ is your perpendicular other is base. This kind of question is used to find the height and distance of things these are for.

Formula used:
$\operatorname{Tan}\theta =\dfrac{Perpendicular}{Base}$

Complete step-by-step answer:

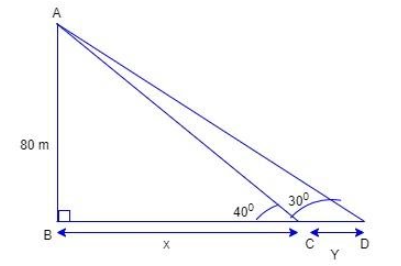
Lighthouse = 80 meters (Given)
Let the distance of ship 1 from the base of the lighthouse = x meters and let the distance between 2 ships = y meters.
Also given that the angle of depression of two ships on the same side of the light house in horizontal line with its base is $40{}^\circ \And 30{}^\circ $ respectively.
$\begin{align}
  & AB=80\text{ }m\left( \text{Height of lighthouse} \right) \\
 & BC=\text{distance of ship }1\text{ from light house base} \\
 & BD=\text{distance of ship 2 from lighthouse base} \\
\end{align}$
$\begin{align}
  & \text{In }\vartriangle \text{ABC} \\
 & \text{tan}\theta \text{=}\dfrac{Perpendicular}{Base} \\
 & \Rightarrow \operatorname{Tan}\theta =\dfrac{AB}{BC} \\
 & \text{by putting the values of }\theta \text{=40}{}^\circ \text{ AB}=80\text{ BC}=x \\
 & \Rightarrow \text{Tan40=}\dfrac{80}{x} \\
 & \Rightarrow \cdot 8391=\dfrac{80}{x} \\
 & BC=\dfrac{80}{\cdot 8391} \\
 & \Rightarrow x=95\cdot 34 \\
\end{align}$
$\begin{align}
  & \text{In }\vartriangle ABD\text{ } \\
 & \text{Tan}\theta \text{=}\dfrac{Perpendicular}{Base} \\
 & \text{putting the values }\theta \text{ 30}{}^\circ \text{ AB}=80,\ \text{BD}=x+y \\
 & \Rightarrow \operatorname{Tan}30=\dfrac{AB}{BD} \\
 & \Rightarrow \dfrac{1}{\sqrt{3}} \\
 & \Rightarrow \dfrac{AB}{~x+y} \\
\end{align}$
\[\begin{align}
  & \Rightarrow x+y=\sqrt{3}\text{ }AB\text{ }\left( \text{Cross Multiplication} \right) \\
 & 95\cdot 34+y=1\cdot 73\times 80\text{ }\left( \text{Substitute Values} \right) \\
\end{align}\]
$\begin{align}
  & \Rightarrow 95\cdot 34+y=138\cdot 56 \\
 & \Rightarrow \text{ }y=138.56-95\cdot 34 \\
 & \Rightarrow \text{ }y=43\cdot 22m\left( \text{approximately} \right) \\
\end{align}$
$\therefore \text{Distance between two ships}=CD=y=43\cdot 22m$
$43m\text{ as answer in nearest metre}$ .

Additional information:
To find the height of a hill, tower, star etc. We can use this formula. This formula is applicable for right angled triangles.

Note: We apply $\text{tan}\theta =$ perpendicular/ base in this we use value of $\tan 40{}^\circ =\cdot 8391$ and we use this formula in two triangles $\vartriangle $ ABC and $\vartriangle $ ABD and simplifying find the value of x and y. Please do mention the units as required in the question as in this question they mentioned that find the answer to the nearest metre.