Question

As more and more awareness is created to keep the city clean, help in reducing pollution, beautifying the city. You must have noticed in Metro and other places of the city, the walls are decorated with art pieces and paintings. One such painting on a wall is in the form of an equilateral triangle of area $49\sqrt 3 {m^2}$. It is noticed that taking each angular point as centre circles have been described with radius equal to half of the length of the side of the triangle. There is some area of the triangular part not included in the circles.
(i) What is the perimeter of an equilateral triangle?
(ii) Find the area of the triangle not included in the circles.

Answer 1

Hint: We will find the side of an equilateral triangle using the given area of the triangle, where area of the triangle is $\dfrac{{\sqrt 3 }}{4}{a^2}$, where $a$ is the side of the equilateral triangle. Then, find the perimeter of the triangle is $3a$. Next, we will subtract the are of the 3 sectors of triangle from the equilateral triangle, where area of the sector is $\dfrac{\theta }{{360}}\pi {r^2}$, where $\theta $ is the angle made by the arc at the centre of the circle and $r$ is the radius of the circle.

Complete step-by-step answer:
We are given that the area of the triangle is $49\sqrt 3 {m^2}$
And we know that the area of the equilateral triangle is given as $\dfrac{{\sqrt 3 }}{4}{a^2}$, where $a$ is the side of the equilateral triangle.
$\Rightarrow$ $\dfrac{{\sqrt 3 }}{4}{a^2} = 49\sqrt 3 $
Divide both sides by $\sqrt 3 $
$\Rightarrow$ $ \dfrac{{{a^2}}}{4}$ = 49
$\Rightarrow$ $ {a^2} = 49\left( 4 \right)$
$\Rightarrow$ $ a = 7\left( 2 \right)$
$\Rightarrow$ $ a = 14$
Thus, the length of the side of an equilateral triangle is 14m.
We have to find the perimeter of the equilateral triangle, which is given by $3a$, where $a$ is the side of the triangle.
Then, $14\left( 3 \right) = 42m$ is the perimeter of the triangle.
In part (ii), we have to calculate the area of the triangle not included in the circles.

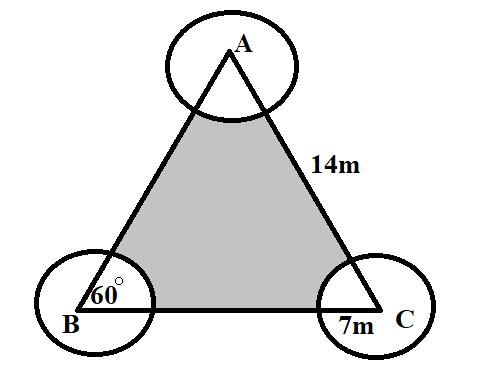
Therefore, we will subtract the area of 3 sectors of circles from the area of the triangle.
We will now calculate the area of the 3 angular circles.
The angle formed at each vertex of the equilateral triangle is ${60^ \circ }$ and radius is half the length of the side of an equilateral triangle.
Thus, the area of 3 circles as the vertex will be
=$3 \times \dfrac{{{{60}^ \circ }}}{{{{360}^ \circ }}}\pi {r^2}$
On substituting the value of $\pi = \dfrac{{22}}{7}$ and $r = \dfrac{{14}}{2} = 7$ in the above expression, we will get,
$\Rightarrow$ $3 \times \dfrac{{{{60}^ \circ }}}{{{{360}^ \circ }}}\left( {\dfrac{{22}}{7}} \right){\left( 7 \right)^2} = 77{m^2}$
Area of the remaining portion will be \[49\sqrt 3 - 77 = 84.87 - 77 = 7.87{m^2}\].

Note: An equilateral triangle is the triangle with equal sides and equal angles of ${60^ \circ }$. The area of an equilateral triangle is $\dfrac{{\sqrt 3 }}{4}{a^2}$ and perimeter is $3a$, where $a$ is the side of the equilateral triangle. The unit of the perimeter is the same as the length of the side and unit of area is measured in square units.