Question

Arrange the given steps in CORRECT order, while constructing $ \Delta PQR $ where $ PM \bot QS $ and it is given that \[QR = 4.2\,cm\] , \[\angle Q = {120^ \circ }\] and \[PQ = 3.5\,cm\] .
Step 1: Now, extend RQ to S and with P as centre and with a sufficient radius, draw an arc, cutting SQ at A and B.
Step 2: Along QX, set off \[PQ = 3.5\,cm\] .
Step 3: Draw a line segment \[QR = 4.2\,cm\] and construct \[\angle RQX = {120^ \circ }\] .
Ste 4: Join PR.
Step 5: Join PC, meeting RQ produced at M. Then, $ PM \bot QS $ .
Step 6: With A as centre and radius more than half AB, draw an arc. Now with B as centre and with the same radius draw another arc, cutting the previous arc at C.
A. $ 1 \to 2 \to 3 \to 4 \to 5 \to 6 $
B. $ 4 \to 1 \to 2 \to 3 \to 5 \to 6 $
C. $ 2 \to 4 \to 3 \to 1 \to 5 \to 6 $
D. $ 3 \to 2 \to 4 \to 1 \to 6 \to 5 $

Answer 1

Hint: Here, in construction of triangle, first we draw lines and angles, if length of side and angle is given. If the sides and angles with common vertex are given, then first draw the angle. Join two vertices when their lengths are fixed. Always cut the length of the segment using a protractor. Draw a rough figure to understand the structure of the triangle asked. Try to draw all given sides, angles etc and then extend the lines whenever required.

Complete step-by-step answer:
All construction steps are arranged in order as below.
Step 1: Draw a line segment \[QR = 4.2\,cm\] and construct \[\angle RQX = {120^ \circ }\] .
Now, a line and an angle has been drawn. We will carry forward with the construction using this as our base.

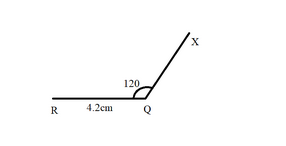
Step 2: Along QX, set off \[PQ = 3.5\,cm\] .
We have already constructed \[\angle RQX = {120^ \circ }\] in the previous step and now we cut off the intercept \[PQ = 3.5\,cm\] on the angle ray.

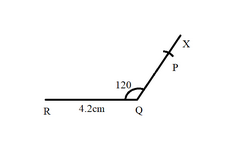
Step 3: Join PR.

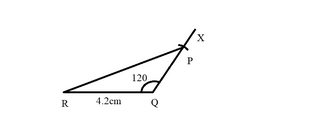
Step 4: Now, extend RQ to S and with P as centre and with a sufficient radius, draw an arc, cutting SQ at A and B.

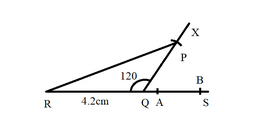
Step 5: With A as centre and radius more than half AB, draw an arc. Now with B as centre and with the same radius draw another arc, cutting the previous arc at C.

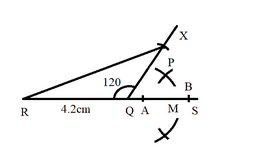
Step 6: Join PC, meeting RQ produced at M. Then, $ PM \bot QS $ .

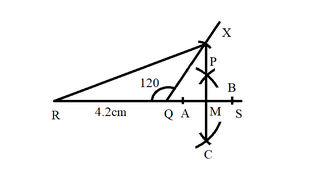
So, this concludes our construction. Following the steps in this order enables us to grasp the reasoning and do the construction analytically.
Hence, option (D) is correct i.e., the correct order is $ 3 \to 2 \to 4 \to 1 \to 6 \to 5 $ .
So, the correct answer is “Option D”.

Note: In construction always start with given as one side is required to draw angle. Whenever you are asked to draw a perpendicular bisector of a line do not just draw a perpendicular line and divide the two half parts using scale, it may have errors. Always take two end points one by one and draw arc above the line and below the line with radius more than half of the length of the line segment, and then join the points of intersections of the arc above the line and below the lines.