Question

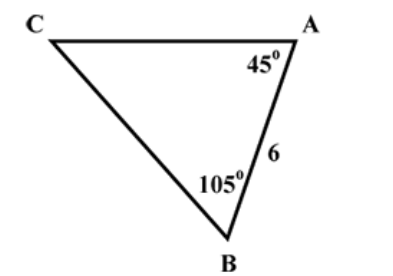
What is the area of the triangle shown in the figure?
 

A. $ 18\sqrt 3 $
B. $ 9 + 9\sqrt 3 $
C. $ 9 + 18\sqrt 3 $
D. $ 18 + 18\sqrt 3 $

Answer 1

Hint: Area is the quantity that expresses the extent of a two-dimensional shape. Let $ \angle C $ as x. The sum of all the angles of the triangle is equal to 180 degrees. Using $ \sin \theta $ to find the area of the triangle. The area of a triangle is a measurement of the area covered by the triangle.

Complete step-by-step answer:
As we know, the sum of all angles inside the triangle will be equal to 180.
In the triangle ABC,
$ \angle A + \angle B + \angle C = {180^ \circ } $
As given in triangle,
$ \angle A = {45^ \circ } $
$ \angle B = {105^ \circ } $
And $ \angle C = x $
Calculate the value of x:
So,
$ \angle C = 180 - (105 + 45) $
$ \angle C = {30^ \circ } $
Using Sine rule,
$ \dfrac{{\operatorname{Sin} A}}{a} = \dfrac{{\operatorname{Sin} C}}{c} $
Keeping value of c = 6
$ \dfrac{1}{{a\sqrt 2 }} = \dfrac{1}{{12}} $
Solving it for a,
$ a = 6\sqrt 2 $
The area of the triangle is given by $ \dfrac{{ac\operatorname{Sin} B}}{2} $
Keeping value in this from above we get,
$ \dfrac{{6\sqrt 2 \times 6 \times \sin {{105}^ \circ }}}{2} $
$ \sin {105^ \circ } $ can also be written as
$ \sin {105^ \circ } = \sin {75^ \circ } = \sin (30 + 45) = \sin {30^ \circ }\cos {45^ \circ } + \sin {45^ \circ }\cos {30^ \circ } $
Used the formula of $ \sin (A + B) $
$ \operatorname{Sin} {105^ \circ } = \dfrac{1}{{2\sqrt 2 }} + \dfrac{{\sqrt 3 }}{{2\sqrt 2 }} $
So I will solve it further. We get,
$ \dfrac{{1 + \sqrt 3 }}{{2\sqrt 2 }} $
Keeping it in area formula,
Thus the area is $ \dfrac{{36\sqrt 2 \times (1 + \sqrt 3 )}}{{4\sqrt 2 }} $ $= 9 + 9\sqrt 3 $
Hence, the area of the triangle is $ 9 + 9\sqrt 3 $. So, the correct option is option (B).

Note: The area of a triangle is a measurement of the area covered by the triangle. The area of a triangle is determined by two formulas i.e. the base multiplies by the height of a triangle divided by 2 and second is Heron’s formula. Heron's formula is a method for calculating the area of a triangle when the lengths of all three sides of the triangle are given. These angles are formed by two sides of the triangle, which meets at a common point, known as the vertex. The sum of all three interior angles is equal to 180 degrees.