Question

What is the area of the hexagon with the sides that are $1.8m$ long?

Answer 1

Hint: The area of the hexagon is calculated by dividing the hexagon into 6 equal triangles as shown below:

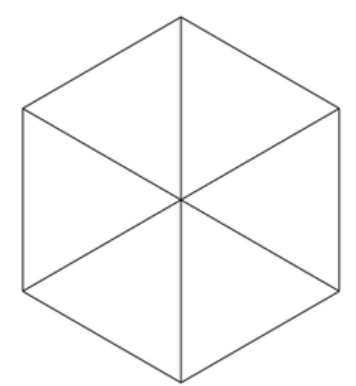
We know that the area of the triangle is given by $\dfrac{1}{2}\times s\times h$, where s is the base of the triangle and h is the height of the triangle. After finding the area of the triangle we can multiply it by 6 to get the area of the hexagon. Since the angle at the centre for the hexagon is ${{360}^{\circ }}$ and all the triangles are equilateral and congruent, therefore when divided into 6 equal parts each has an angle of ${{60}^{\circ }}$ .

Complete step by step solution:
We have been given that the sides of the hexagon are $1.8m$ long.
We have to find the area of the hexagon.
Let us consider a hexagon and divide it into six equal parts as shown below:

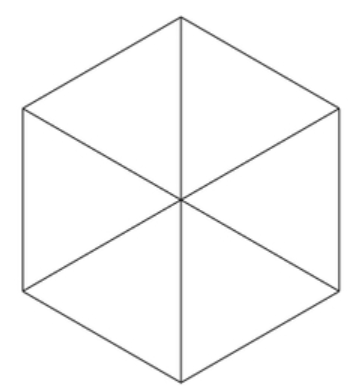
Now since the angle at centre is ${{360}^{\circ }}$ therefore we can say that angle for each triangle will be ${{60}^{\circ }}$.
Since the triangle is equilateral, we know that all the sides and angles are equal.
If we draw a median on side BC such that it bisects the triangle into two equal part and is perpendicular to the base we have:

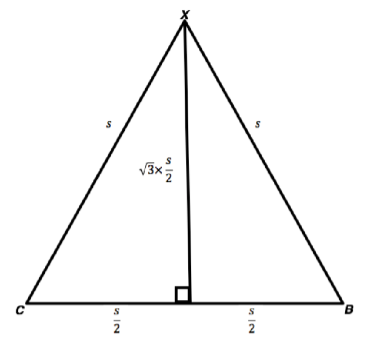
Since from Pythagoras Theorem we have:
${{H}^{2}}={{P}^{2}}+{{B}^{2}}$
$\begin{align}
  & {{h}^{2}}={{s}^{2}}-{{\left( \dfrac{s}{2} \right)}^{2}} \\
 & h=\dfrac{\sqrt{3}s}{2} \\
\end{align}$
Now, we have the side as 1.8m, so
$h\approx 1.56m$
Using the formula, we get that the area of triangle is given by:
$\dfrac{1}{2}\times s\times h$
Now, substituting, we get
$\begin{align}
  & A=\dfrac{1}{2}\times 1.8\times 1.56 \\
 & A=1.404{{m}^{2}} \\
\end{align}$
We can find the area of the hexagon as $6A$. Hence, we get
$6\times 1.404=8.42{{m}^{2}}$
The area of the hexagon is $8.42{{m}^{2}}$.

Note: There is another method to solve this question by using the formula for finding the area of the hexagon.
$A=\dfrac{3\sqrt{3}}{2}{{s}^{2}}$
If we substitute the value of side we get,
$\begin{align}
  & A=\dfrac{3\sqrt{3}}{2}\times {{1.8}^{2}} \\
 & A\approx 8.42{{m}^{2}} \\
\end{align}$
Thus, the value obtained is similar to that obtained above hence either of the methods could be used.