Question

What is the area of the circular ring included between two concentric circles of radius 14cm and 10.5 cm.

Answer 1

Hint:Start by drawing a representative diagram of the situation given in the question.Use the area of the circle with the larger radius and subtract the area of the other circle to reach the answer.

Complete step-by-step answer:
Let us start by drawing the representative diagram of the situation given in the question.

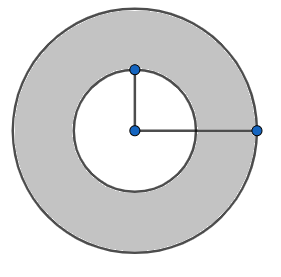
Now from the figure it is clear that we need to find the area of the shaded region.
First, we will find the area of the circle with radius 14 cm.
$\therefore \text{Area of the larger circle = }\pi {{\text{r}}^{2}}=\pi \times {{14}^{2}}=196\pi \text{ c}{{\text{m}}^{2}}$
Similarly, we will find the area of the circle with radius 10.5 cm.
$\therefore \text{Area of the smaller circle = }\pi {{\text{r}}^{2}}=\pi \times {{\left( 10.5 \right)}^{2}}=110.25\pi \text{ c}{{\text{m}}^{2}}$
 Now moving to find the area of the shaded region. As you can see in the figure that the area of the shaded region is the area of the larger circle minus the area of the smaller circle.
$\therefore \text{Area of the ring = Area of the large circle - Area of the small circle}$
$\therefore \text{Area of the ring = 196}\pi \text{-110}\text{.25}\pi \text{=85}\text{.75}\pi \text{ c}{{\text{m}}^{2}}$
Now we will put the value of $\pi $ to be $\dfrac{22}{7}$ . On doing so, we get
$\therefore \text{Area of the ring = 85}\text{.75}\times \dfrac{22}{7}=269.5\text{ c}{{\text{m}}^{2}}$
Hence, the answer to the above question is 269.5 square cm.

Note: It is prescribed to learn all the basic theorems related to circles as they are regularly used in the questions related to circles and triangles, as we did in the above question. Also, learn all the formulas related to the area and perimeter of the circle.