Question

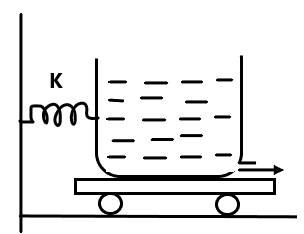
Area of muzzle is A. Due to ejection of water (density $ = \rho $ ) at a velocity $ v $ , the compression in spring at equilibrium is:

(A) $ \dfrac{{\rho A{v^2}}}{{2K}} $
(B) $ \dfrac{{\rho A{v^2}}}{K} $
(C) $ \dfrac{{2\rho A{v^2}}}{K} $
(D) $ \dfrac{{4\rho A{v^2}}}{K} $

Answer 1

Hint : Fundamentally, Newton’s second law states that force is directly proportional to the rate of change of momentum with time. In terms of fluid, even at constant velocity, the rate of flow of mass constitutes a changing momentum. In equilibrium, the force due to ejection of mass is equal to the force exerted by the spring due to change in length.

Formula used: In this solution we will be using the following formula;
 $ \Rightarrow F = \dfrac{{dp}}{{dt}} $ where $ F $ is the force acting on a body, $ p $ is the momentum, and $ t $ is time.
 $ \Rightarrow p = mv $ , where $ m $ is mass, and $ v $ is velocity.
 $ \Rightarrow \dfrac{{dm}}{{dt}} = \rho Av $ where $ \dfrac{{dm}}{{dt}} $ is called the mass flow rate, $ \rho $ is the density, and $ A $ is the cross sectional area.
 $ \Rightarrow {F_s} = Ke $ where $ {F_s} $ is the force exerted by a spring, $ K $ is the force constant (also called spring constant) and $ e $ is the extension or compression of the spring from equilibrium.

Complete step by step answer
During the ejection of the water, by Newton’s third law, the force exerted on the water in the rightward direction is equal to the force exerted on the vessel in the leftward direction.
Now, the force on the water is
 $ \Rightarrow F = \dfrac{{dp}}{{dt}} = \dfrac{{d\left( {mv} \right)}}{{dt}} = v\dfrac{{dm}}{{dt}} $ ( since $ p = mv $ )
 $ \Rightarrow F = v\rho Av = pA{v^2} $ ( because $ \dfrac{{dm}}{{dt}} = \rho Av $ where $ \dfrac{{dm}}{{dt}} $ is called the mass flow rate, $ \rho $ is the density, and $ A $ is the cross sectional area)
Now, in equilibrium, this force is equal to the force exerted by the spring, hence,
 $ \Rightarrow {F_s} = pA{v^2} $
But $ {F_s} = Ke $ where $ {F_s} $ is the force exerted by a spring, $ K $ is the force constant (also called spring constant) and $ e $ is the extension or compression of the spring from equilibrium.
Hence,
 $ \Rightarrow Ke = pA{v^2} $
 $ \Rightarrow e = \dfrac{{pA{v^2}}}{K} $
Hence, the correct option is C.

Note
For clarity, we can prove that $ \dfrac{{dm}}{{dt}} = \rho Av $ accordingly.
 $ \Rightarrow m = \rho V $ where $ V $ is the volume.
But $ V = Ax $ , where $ x $ is the distance of the muzzle from the front end of the water.
hence
 $ \Rightarrow dm = \rho Adx $ ,then
 $ \Rightarrow \dfrac{{dm}}{{dt}} = \rho A\dfrac{{dx}}{{dt}} = \rho Av $ .