Question

What is the area of an equilateral triangle with side length $14?$

Answer 1

Hint: We know that an equilateral triangle is a triangle whose all three sides are equal. The measure of each interior angle is ${60^ \circ }$. So the sum of all the angles of the triangle is ${180^ \circ }$. We can calculate the area of an equilateral triangle if its sides are known. The area of an equilateral triangle is $\dfrac{{\sqrt 3 }}{4}{a^2}$, where $a$ is the side of the triangle.

Complete step by step solution:
Here we have the length of the side of an equilateral triangle i.e. $14$.
We know that the area of an equilateral triangle is $\dfrac{{\sqrt 3 }}{4}{a^2}$, here we have $a = 14$.

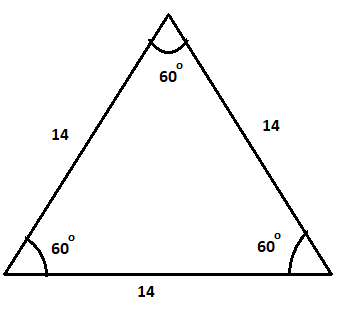
So now putting the value in the formula, we can write $A = \dfrac{{\sqrt 3 }}{4} \times 14 \times 14$. On further solving it gives us the value $A = 7 \times 7 \times \sqrt 3 = 49\sqrt 3 $.
Hence, the area of the equilateral triangle is $49\sqrt 3 $.

Note:
We can also take the decimal value of $\sqrt 3 $ in the formula of area i.e. $\sqrt 3 = 1.732$. So the area will be $1.732 \times 49 = 84.9(approx)$. We should know that the perimeter of an equilateral is $3a$, where $a$ is the length of the side. We can find the altitude of an equilateral triangle by $h = \dfrac{{\sqrt 3 }}{2}a$.