Question

What is the area of a triangle with the base $4.8cm$ and height $3.6cm$

Answer 1

Hint: We are given the base and height of the triangle and we need to find the area of the triangle. The area of a triangle is the total space occupied by the three sides of the triangle. The basic formula for the area of a triangle is equal to half the product of its base and height.
Formula: Area of the triangle = $\dfrac{1}{2}\left( {base \times height} \right)square{\text{ }}units$
It can also be written as, Area of the triangle = $\dfrac{1}{2}\left( {b \times h} \right)square{\text{ }}units$

Complete step-by-step answer:
Given that the length of base (b) = $4.8cm$, height (h) = $3.6cm$. The length of base and height of the triangle are in $cm$. So we don’t need to convert in a single unit as already they both have the same unit.
Let us construct a triangle with a base $4.8cm$ and $3.6cm$.

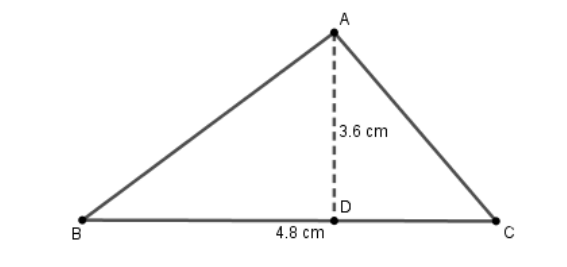
Now, we have a triangle ABC with vertices A, B, and C. The three sides of a triangle are AB, BC, and CA. Side BC is the base of the triangle. AD is the height of the triangle.
Formula: Area of the triangle = $\dfrac{1}{2}\left( {b \times h} \right)square{\text{ }}units$
Area of triangle ABC = $\dfrac{1}{2} \times BC \times AD$
As we know for triangle ABC, base (BC) = $4.8cm$ and height (AD) = $3.6cm$
Area of triangle ABC = $\dfrac{1}{2} \times 4.8cm \times 3.6cm$
It can also be written as:
Area of triangle ABC = $\dfrac{1}{2} \times 4.8 \times 3.6c{m^2}$
Area of triangle ABC = $\dfrac{1}{2} \times 17.28c{m^2}$
Area of triangle ABC = $8.64c{m^2}$
Thus the area of the triangle ABC with base $4.8cm$ and height $3.6cm$ is $8.64c{m^2}$.
So, the correct answer is “$8.64c{m^2}$”.

Note: We should be careful about the unit. The calculation should be done in the same unit. We should take care of the calculations so as to be sure of our final answer. There are other formulae too to find the area of the triangle.
For example:
Area of a right-angled triangle = $\dfrac{1}{2} \times base \times height$
Area of an equilateral triangle = \[\dfrac{{\sqrt 3 }}{4} \times sid{e^2}\]
Area of an isosceles triangle = $\dfrac{1}{4} \times b \times \sqrt {4{a^2} - {b^2}} $ ($b$ is the base and $a$ is the measure of one of the equal sides.