Question

What is the area of a semicircle with a radius $8\,cm$ ?

Answer 1

Hint: We know that when we cut the circle diametrically into two halves, one half is known as semicircle. This means that half of a circle is a semicircle and also the area of a semicircle is half that of a circle. So, we can use the formula $\dfrac{{\pi {r^2}}}{2}$ to find the area of semicircle, where $\pi {r^2}$ is the formula of circle whose radius is r.

Formula used: Area of semicircle $ = \,\dfrac{{\pi {r^2}}}{2}$ .

Complete step by step answer:
A semicircle is a half-circle that is formed by cutting a whole circle into two halves along a diameter line. A line segment known as the diameter of a circle cuts the circle into exactly two equal semicircles.

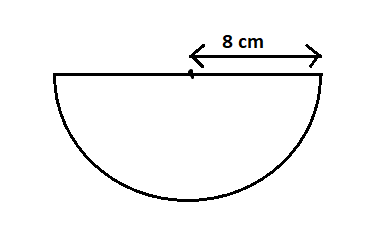
Hence, the area of a semicircle is half the area of a circle.
The area of a semicircle or the area of a half circle is $\dfrac{{\pi {r^2}}}{2}$, where r is the radius of the semicircle.
Therefore,
Area of semicircle $ = \,\dfrac{{\pi {r^2}}}{2}$
Now, putting the value of r from the given question as $r = 8\,cm$.
Area of semicircle $ = \,\dfrac{{\pi {{\left( 8 \right)}^2}}}{2}$
Now putting the value of $\pi = 3.14$
$ \Rightarrow \dfrac{{3.14{{\left( 8 \right)}^2}}}{2}$
$ \Rightarrow \dfrac{{3.14 \times 64}}{2}$
$ \Rightarrow 3.14 \times 32$
$ \therefore 100.48\,c{m^2}$
Hence, the area of the semicircle is $100.48\,c{m^2}$.

Note: The semicircle is also referred to as a half-disk. Since the semicircle is half of the circle (\[360\] degrees), the arc of the semicircle always measures \[180\] degrees. The perimeter of a semicircle is $\pi r + 2r$, which can also be written as $r\left( {\pi + 2} \right)$ by factoring out r.