Question

What is the area of a circle with diameter, $ d = 3.4m $ ?

Answer 1

Hint: The area of a flat shape or the surface of an object may be described in geometry as the space occupied by it. The number of unit squares that cover the surface of a closed figure is the figure's area.
Formula Used:
 $ A = \pi {r^2} $
Here,
 $ A $ is the area and
 $ r $ is the radius.

Complete step-by-step answer:

The area of a circle is defined as the area enclosed or the space occupied by a circle with a radius $ r $ . The area of a circle is given by the formula $ \pi {r^2} $ . The Greek letter $ \pi $ reflects the constant circumference-to-diameter ratio of any circle, which is roughly 3.1416.
A straight line passing through the centre of the circle is the diameter. Half of the diameter is the radius. It begins at a point on the circle and ends at the circle's middle.
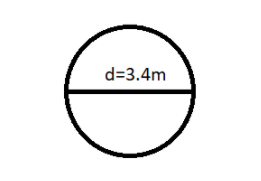
Here the diameter of the circle is given, which is $ 3.4m $ .
So, the radius of the circle has to be found out. The radius is given by the expression:
 $ r = \dfrac{d}{2} $ ,
Thus, $ r = \dfrac{{3.4}}{2} = 1.7 $ .
By substituting the value of r, the Area can be a found out:
 $ A = \pi {r^2} $
 $ A = (3.14){(1.7)^2} $
 $ A = 9.07{m^2} $
Thus, the area of a circle with diameter $ d = 3.4 $ is $ 9.07{m^2} $ .
So, the correct answer is “ $ 9.07{m^2} $ ”.

Note: The basic unit of area in the International System of Units (SI) is the square metre (represented as $ {m^2} $ ), which is the area of a square with sides that are one metre long. A three-square-metre shape has the same area as three squares of the same size.