Question

What is the area of a circle if the diameter is 9 cm?

Answer 1

Hint: We solve this question by using the basic formula for finding the area of a circle. This formula is given as $A=\pi {{r}^{2}}.$ Here, A represents the area of the circle and r is the radius of the circle. We represent this formula in terms of diameter as $A=\pi {{\left( \dfrac{d}{2} \right)}^{2}}=\dfrac{\pi {{d}^{2}}}{4}.$ Using this, we substitute the given value of diameter as 9 cm and find the area of the circle in $c{{m}^{2}}.$

Complete step by step solution:
In order to solve this question, let us write the formula for calculating the area of a circle. This is given by,
$\Rightarrow A=\pi {{r}^{2}}$

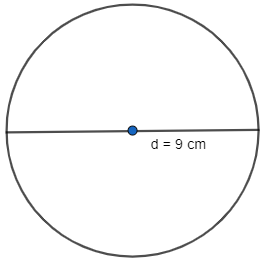
Here, r is the radius of the circle and A is the area of the circle. We know the relation between the diameter and radius of a circle is given as,
$\Rightarrow r=\dfrac{d}{2}$
This means that the radius of a circle is equal to half of its diameter. Using this relation in the above formula,
$\Rightarrow A=\pi {{\left( \dfrac{d}{2} \right)}^{2}}$
Squaring the term and writing it,
$\Rightarrow A=\dfrac{\pi {{d}^{2}}}{4}$
Now, we are given the value of the diameter as 9 cm. We substitute this in the above equation as follows,
$\Rightarrow A=\dfrac{\pi \times {{9}^{2}}}{4}$
We know the value of $\pi =3.1415$ and calculating the square of 9, we get
$\Rightarrow A=\dfrac{3.1415\times 81}{4}$
Multiplying the terms in the numerator and dividing by 4, we get
$\Rightarrow A=63.62c{{m}^{2}}$

Hence, the area of a circle if the diameter is 9 cm is $63.62c{{m}^{2}}.$

Note:
We need to know the basic formulae for finding the area of a circle in order to solve this question. We can also solve this question by dividing the diameter by 2 and calculating the radius and substituting in the formula $A=\pi {{r}^{2}}$ to calculate the area of the circle. Both yield the same results.