Question

What is the area of \[{45^ \circ } - {45^ \circ } - {90^ \circ }\] triangle with a hypotenuse of 8mm in length?

Answer 1

Hint: Here given is a triangle that has two angles the same and the remaining angle is of \[{90^ \circ }\] . We know that the ratio of sides of the triangle is \[1:1:\sqrt 2 \]. To get the area of the triangle we should know the base and height length. So we will use the formula as \[hypt = l\left( {base} \right) \times \sqrt 2 \] to find the length of base and will be the same as height. And then the area formula.
Formula used:1.
I.\[area = \dfrac{1}{2} \times base \times height\]
II.\[hypt = l\left( {base} \right) \times \sqrt 2 \]

Complete step-by-step answer:
Given is a triangle of measure \[{45^ \circ } - {45^ \circ } - {90^ \circ }\]

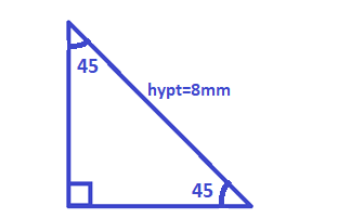
Now we know that formula for finding the length of base or height,
\[hypt = l\left( {base} \right) \times \sqrt 2 \]
Putting the value of hypotenuse we get,
\[8 = l\left( {base} \right) \times \sqrt 2 \]
On dividing we get,
\[l\left( {base} \right) = \dfrac{8}{{\sqrt 2 }}\]
Now we can write the numerator as,
\[l\left( {base} \right) = \dfrac{{2\sqrt 2 \times 2\sqrt 2 }}{{\sqrt 2 }}\]
Now cancelling the root,
\[l\left( {base} \right) = 4\sqrt 2 \]
This is the base length as well as the height length.
Now to find the area we will use the formula of area,
\[area = \dfrac{1}{2} \times base \times height\]
\[area = \dfrac{1}{2} \times 4\sqrt 2 \times 4\sqrt 2 \]
On dividing by 4 we get,
\[area = 2\sqrt 2 \times 4\sqrt 2 \]
On multiplying the root will be removed as,
\[area = 2 \times 2 \times 4\]
Now the area is,
\[area = 16\;m{m^2}\]
Tus this is the area of the triangle so given.
So, the correct answer is “\[area = 16\;m{m^2}\]”.

Note: Note that the triangle is an isosceles triangle but the formula to find the area is the same. Also note that the relation between the hypotenuse and the side of the triangle is this only for a \[{45^ \circ } - {45^ \circ } - {90^ \circ }\] triangle and not any other triangle.