Question

Area bounded by \[y\left| y \right|-x\left| x \right|=1,y\left| y \right|+x\left| x \right|=1\] and \[y=\left| x \right|\] is
A. \[\dfrac{\pi }{2}\]
B. \[\pi \]
C. \[\dfrac{\pi }{4}\]
D. None of these

Answer 1

Hint:Now there are many methods to solve the question, but we use the graphical method. First we plot all the graphs of the equation given in the equation as:
\[y\left| y \right|-x\left| x \right|=1,y\left| y \right|+x\left| x \right|=1\ and y=\left| x \right|\] with the graphs marked as colour of red, blue and green respectively as shown below.

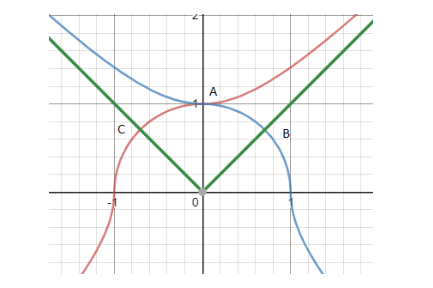
Complete step by step solution:
First find the coordinates in the graph where any two graphs are intersecting and then we find the integration of the three equations to find the area of the figure ABCD. Hence, we use the integration formula where we use the formula in terms of\[y\]:
First we find the equations in terms of \y\ for all the equation as:
\[y=\sqrt{1+x\left| x \right|}\, y=\sqrt{1-x\left| x \right|}\] and \[y=\left| x \right|\] and then we put the values of \[y\] in the formula given below as:
\[\Rightarrow \int\limits_{y}^{x}{\sqrt{1+x\left| x \right|}}+\int\limits_{B}^{A}{\sqrt{1-x\left| x
\right|}}+\int\limits_{b}^{a}{\left| x \right|}\]
Now we have put together a term for the area of the figure ABCD and to find the value of the area we will first find the limit of the points A,B,C and D. First let us equate \[y\left| y \right|+x\left| x \right|=1\
and \,y=\left| x \right|\]:
\[\Rightarrow y\left| y \right|+x\left| x \right|=1\ with \,y=\left| x \right|\]
\[\Rightarrow \left| x \right|\left| \left| x \right| \right|+x\left| x \right|=1\]
\[\Rightarrow {{x}^{2}}+{{x}^{2}}=1\]
\[\Rightarrow 2{{x}^{2}}=1\]
\[\Rightarrow x=\sqrt{\dfrac{1}{2}}\]
\[\Rightarrow x=\pm 0.707\] and with \[y=\left| x \right|\], we get the value of \[y=\pm 0.707\],
giving us the coordinates as:
C\[\left( -0.707,0.707 \right)\], B \[\left( 0.707,0.707 \right)\], D \[\left( 0,0 \right)\] and A\[\left( 1,1
\right)\].
Now placing the pointers in the above equation as:
\[\Rightarrow \int\limits_{0}^{-0.707}{\sqrt{1+x\left| x \right|}}+\int\limits_{0}^{0}{\sqrt{1-x\left| x
\right|}}+\int\limits_{0.707}^{0}{\left| x \right|}\]
Integrating the values of the integrations given above, we get the value of the area of ABCD as:
\[\Rightarrow \left[ \dfrac{{{\sin }^{-1}}x}{2}+\dfrac{x\sqrt{{{x}^{2}}+1}}{2} \right]_{0}^{-0.707}+\left[
\dfrac{{{\sin }^{-1}}x}{2}+\dfrac{x\sqrt{1-{{x}^{2}}}}{2} \right]_{0}^{0}+\dfrac{x\left| x
\right|}{2}_{0.707}^{0}+C\]
\[\Rightarrow \dfrac{\dfrac{\pi }{4}}{2}+\dfrac{-0.707\sqrt{0.5+1}}{2}+0+0-\dfrac{0.5}{2}\]
Changing the values of $\pi =3.14$ we get the final result as:
\[\Rightarrow \dfrac{3.14}{8}+\dfrac{-0.707\sqrt{0.5+1}}{2}-\dfrac{0.5}{2}\]
\[\Rightarrow \dfrac{3.14}{8}+\dfrac{-0.707\sqrt{0.5+1}}{2}-\dfrac{0.5}{2}\]
\[\Rightarrow 0.58\]unit square.
Therefore, the area of the figure ABCD is given as \[0.58\] unit square.

Note: When such questions are given point out the marks that are forming the enclosed area, and then find the area by integration of the equations given, the pointers or the limit are the x-coordinates.