Question

Area bounded by the curve $y={{\log }_{e}}x$, $x=0,y\le 0$ and $x$ axis is
(a) 1
(b) $\dfrac{1}{2}$
(c) 2
(d) None of the above

Answer 1

Hint: Area is always positive, so don’t forget to attach a modulus to whatever integral you get for the area. The graph of $y={{\log }_{e}}x$ extends till $y=-\infty $, and hence it doesn’t cut the $y$ axis anywhere. However, work with the value of $x$, which will range from 0 to 1, since after$x=1$, the function gives positive value, and the condition $y\le 0$ won’t be satisfied. Thus, your lower and upper limits will be $x=0$and 1 respectively.

Complete Step-by-Step solution:
First of all, try imagining the graph of the function $y={{\log }_{e}}x$, because only then will you understand which portion exactly you need to find the area of.
Now, we’re told that the limits of this integral are the $y$ axis or $x=0$, all the non positive values of $y$, or $y\le 0$ and the $x$ axis.
Now, let’s see what the graph of $y={{\log }_{e}}x$ looks like.

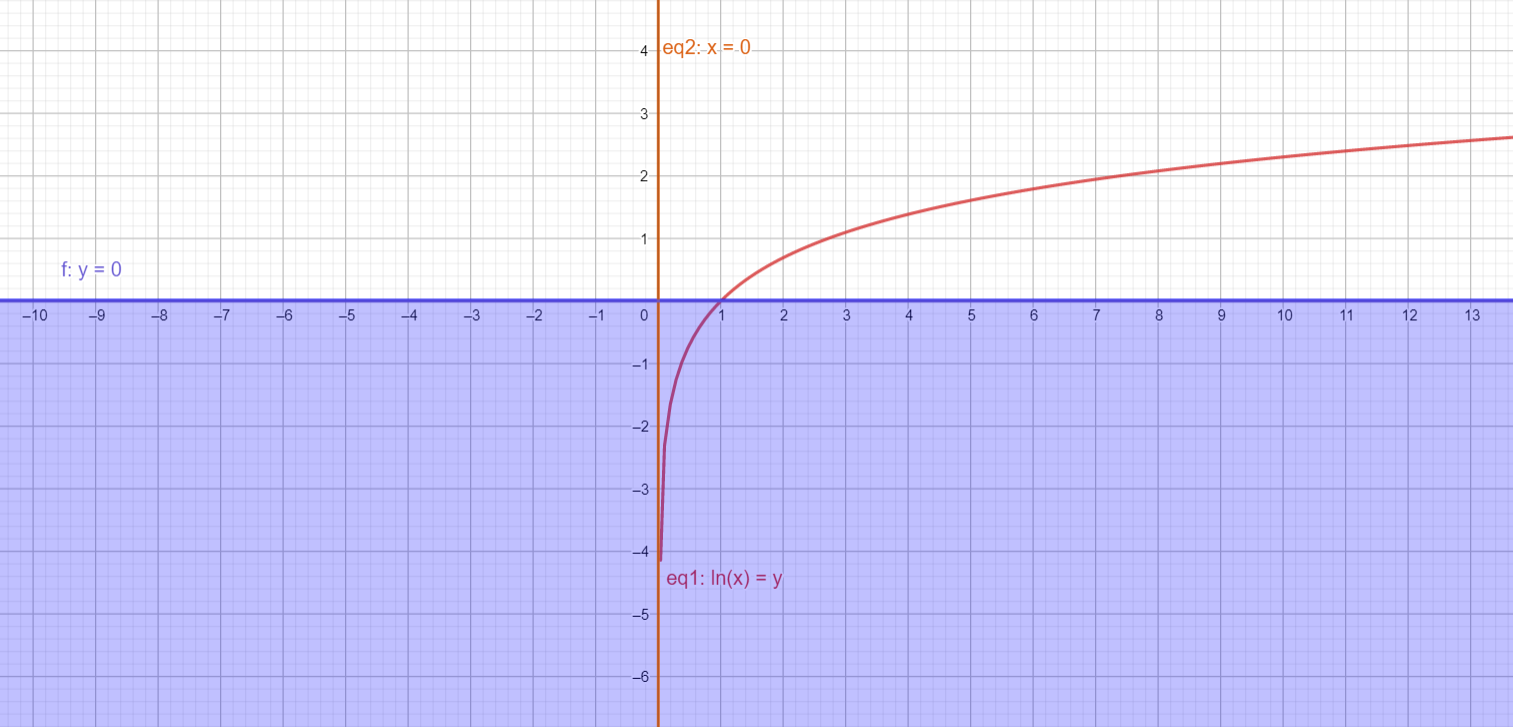
The violet shaded region shows $y\le 0$, and as you can see, the graph of $y={{\log }_{e}}x$ does not intersect with the $y$ axis anywhere. Instead, it goes on till $y=-\infty $. Now, we can see which region we need to find the area of.
The required area is enclosed between $x=0$ and $x=1$, simply because the graph extends till $y=-\infty $ and cuts the $x$ axis at $x=1$. This gives us the lower limit of the integral as 0, and the upper limit as 1.
Therefore, the required area of any curve $f(x)$ is represented by $|\int\limits_{x=a}^{x=b}{f(x)dx}|$ , since we want the value of the area, or the unsigned value, provided, that $x=a$ is the lower limit of the region we need to find the area of, and $x=b$ is the upper limit.
Hence, we can apply the same logic here, and thus, our required area = $|\int\limits_{x=a}^{x=b}{f(x)dx|=|\int\limits_{x=0}^{x=1}{f(x)dx}}|$
In our case, our $f(x)={{\log }_{e}}x$, and hence, substituting, we get :
$|\int\limits_{x=0}^{x=1}{{{\log }_{e}}xdx|=}|\int\limits_{x=0}^{x=1}{\ln xdx|}$
Now, to solve this integral, we need to apply the rule of integration by parts.
In this rule, when we have a function that is made by the multiplication of two other functions, we can assign one function as function (I) and the other as function (II).
Then, the integral becomes :
\[\int\limits_{a}^{b}{f(x).g(x)dx=}\int\limits_{a}^{b}{\overset{I}{\mathop{f(x)}}\,.\overset{II}{\mathop{g(x)}}\,dx=}[f(x)\int{g(x)dx]_{a}^{b}-\int\limits_{a}^{b}{\dfrac{df(x)}{dx}.\int{g(x)dx)}}}dx\]
Here, we assume $f(x)$ as function (I) and $g(x)$ as function (II). And thus, this formula depends on which function you choose as (I) and which one as (II).
For this question, let’s consider $f(x).g(x)={{\log }_{e}}x=\ln x$
Now, to apply integration by parts, we need to select the first function and second function respectively. Let’s consider $\ln x$ as the first function, and 1 as the second function. This is done because after all, $\ln x=1.\ln x$.
Thus, applying the formula of integration by parts, we get :
$\begin{align}
  & \int\limits_{x=0}^{x=1}{\overset{II}{\mathop{1}}\,.\overset{I}{\mathop{\ln x}}\,dx}=([\ln x].\int{1dx})_{0}^{1}-\int\limits_{0}^{1}{(\dfrac{d(\ln x)}{dx}.\int{1dx)dx}} \\
 & =(x\ln x)_{0}^{1}-\int\limits_{0}^{1}{\dfrac{1}{x}.xdx} \\
 & =[0-0]-(x)_{0}^{1} \\
 & =-(1-0)=-1 \\
\end{align}$
Thus, we have the value of $\int\limits_{x=0}^{x=1}{\ln xdx=-1}$. However, we have been asked for the area enclosed by the graph of $\ln x$, and the area can never be negative. So, we have to take the modulus of this value, which will be $|\int\limits_{x=0}^{x=1}{\ln xdx|=|-1|=1}$.
Hence, the area is option a, 1.
option (a) is Correct.

Note: You might get confused regarding when to take the modulus of the integral and when to not take the integral. In this question we were asked for an area that is all negative, so it was safe to put the modulus over the entire integral. However, when we are asked to find the area of a graph that lies both in the positive $y$ as well as the negative $y$ region, we have to break the integral at the points where the function changes its value from negative to positive and vice versa. This is done because while calculating the integral, we’ll get a negative value for the area that lies below the $y$ axis. But, we have to carefully take the modulus of the negative area, since area can never be negative, and the total area can only be the sum of the areas of the required regions, immaterial of whether they lie in the positive $y$ or the negative $y$ region. Therefore, you should be very careful about the modulus, and break the function at the places when the function’s value changes from positive to negative or the other way round.