Question

What are the radius and curved surface area of a cone made from a quadrant of a circle of radius 28 cm?

Answer 1

Hint: In this particular question use the concept that the curved surface area of the cone is equal to the area of the quadrant of the circle and use the concept that the slant height of the cone is equal to the radius of the circle so use these concepts to reach the solution of the question.

Complete step-by-step solution:

Given data:
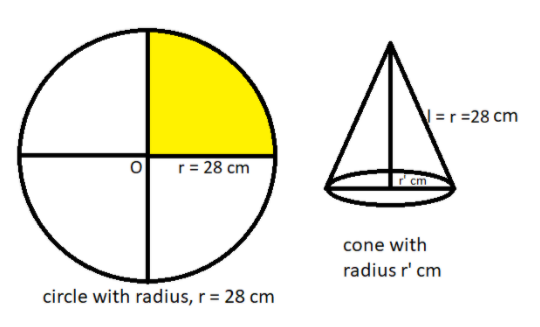
The radius of the circle, r = 28 cm.
As we know that the area of the circle is given as $\pi {r^2}$ square units where r is the radius of the circle.
As we all know that the area of the quarter of the circle is (1/4) times the area of the circle as shown in the figure marked with yellow color.
So, area of the quarter of the circle = $\dfrac{{\pi {r^2}}}{4} = \dfrac{{\dfrac{{22}}{7}{{\left( {28} \right)}^2}}}{4} = 22\left( {28} \right) = 616{\text{ c}}{{\text{m}}^2}$, $\left[ {\because \pi = \dfrac{{22}}{7}} \right]$
Now the cone is made of the quadrant of the circle, so the curved surface area of the cone is equal to the area of the quadrant of the circle.
Therefore the curved surface area (CSA) of the cone = 616${cm}^2$.
Now as we know that the formula of the CSA of the cone = $\pi r'l$ square units, where r’ and l is the radius and slant height of the cone respectively.
Now the slant height of the cone is equal to the radius of the circle.
Therefore, l = r = 28 cm.
Therefore, CSA = $\pi r'l$
Now substitute the values we have,
$ \Rightarrow 616 = \dfrac{{22}}{7}\left( {r'} \right)\left( {28} \right)$
$ \Rightarrow \dfrac{{616 \times 7}}{{28 \times 22}} = r'$
$ \Rightarrow r' = 7$ cm
So the radius and CSA of the cone is 7 cm and 616${cm}^2$.
So this is the required answer.

Note: Whenever we face such types of questions the key concept we have to remember is that always recall the formula of the curved surface area of the cone in terms of slant height and radius of the cone which is stated above and also recall the formula for the area of the circle so the area of the quadrant of the circle is (1/4) times the area of the circle.