Question

How are the graphs $f\left( x \right)={{x}^{3}}$ and $g\left( x \right)={{\left( x+2 \right)}^{3}}-5$ related?

Answer 1

Hint: Here in this question we have been asked to explain the relation between the graphs for $f\left( x \right)={{x}^{3}}$ and $g\left( x \right)={{\left( x+2 \right)}^{3}}-5$ . Let us consider that the curve of the function $f\left( x \right)$ has the curve positioned at the origin.

Complete step by step solution:
Now considering from the question we have been asked to explain the relation between the graphs for $f\left( x \right)={{x}^{3}}$ and $g\left( x \right)={{\left( x+2 \right)}^{3}}-5$ .
For answering this question let us consider that the curve of the function $f\left( x \right)$ has the curve positioned at the origin.
The graph of $f\left( x \right)$ has been illustrated below:

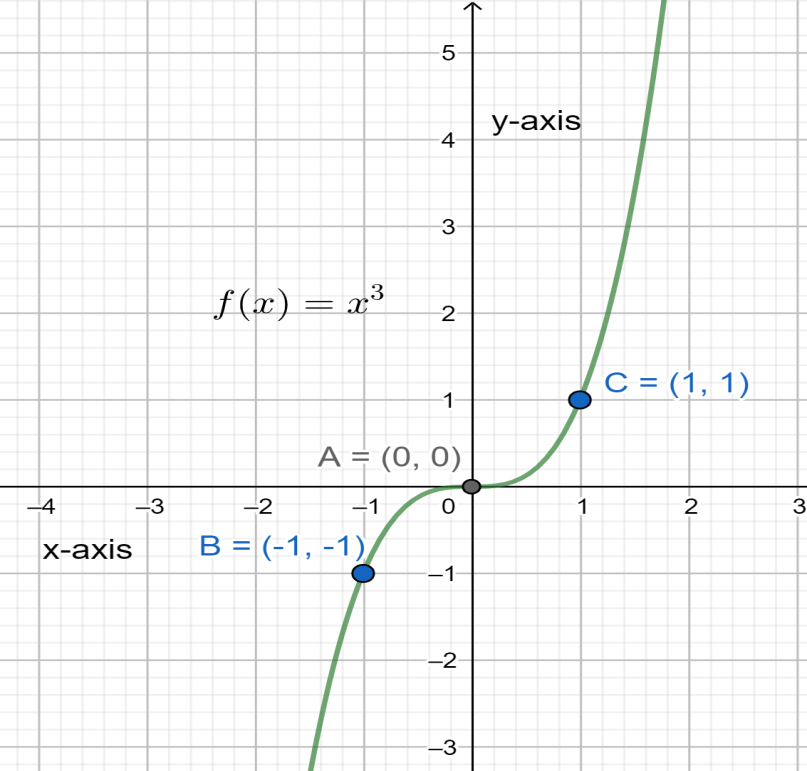
Now $g\left( x \right)$ can be simple written as $g\left( x \right)=f\left( x+2 \right)-5$ since $f\left( x+2 \right)={{\left( x+2 \right)}^{3}}$ . By observing this we can say that $f\left( x \right)$ has been shifted by 2 horizontally left and 5 vertically down for obtaining the graph of $g\left( x \right)$ .
The graph of $g\left( x \right)$ has been illustrated below:

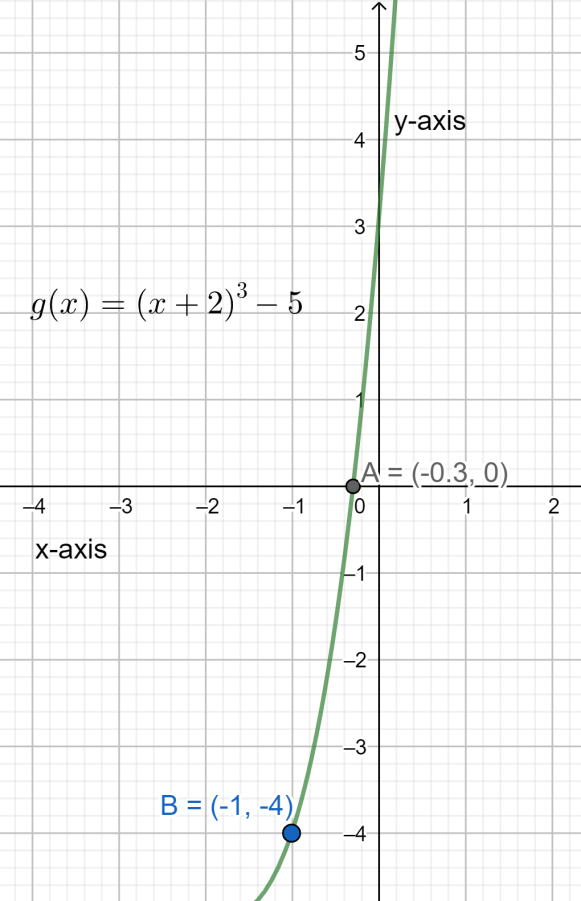
Therefore we can conclude that the function $g\left( x \right)$ has been formed by shifting the curve of the function $f\left( x \right)$ horizontally to the left by 2 and vertically down by 5.

Note: During the process of answering questions of this type we should be sure with the concepts that we are going to apply in between. This is a very simple and easy question and can be answered accurately in a short span of time. Very few mistakes are possible in questions of this type. Someone can make a mistake unintentionally and consider the simplification as $g\left( x \right)=f\left( x \right)+5$ which will lead them to end up having a wrong conclusion.