Question

What are the dimensions of the circle? $Area=64\pi \,i{{n}^{2}}$ .

What is r?

Answer 1

Hint: The equation to find the cross sectional area of a circle is given as $Area=\pi {{r}^{2}}$ , where r is the radius of the circle. Use this formula to solve this problem.

Complete step by step answer:
In the question we have been given the area of the circle as $Area=64\pi \,i{{n}^{2}}$, where the unit is square inches. We can use the formula for the area of a circle in terms of its radius to solve this problem. Therefore, we get,
$\begin{align}
  & \,\,\,Area=\pi {{r}^{2}} \\
 & \Rightarrow \pi {{r}^{2}}=64\pi \\
 & \,\,\,\Rightarrow {{r}^{2}}=64\,i{{n}^{2}} \\
\end{align}$
After obtaining ${{r}^{2}}$ , we can find its roots by taking square root.
$\begin{align}
  & \Rightarrow r=\pm \sqrt{64} \\
 & \Rightarrow r=\pm 8\,\,in \\
\end{align}$
Since, the radius of a circle is a positive quantity, it is meaningless to take a negative value. Hence,
$r=8\,\,in$
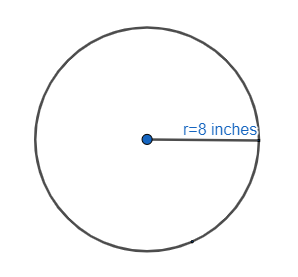
Therefore, the radius of the given circle is found to be 8 inches. The resulting circle with the dimensions is as shown in the figure.

Note: While solving this problem, in case the ${{r}^{2}}$ value does not turn out to be a perfect square, then we can find the square root by calculating manually, or by using a calculator. For example, if the area was given as $2\pi \,i{{n}^{2}}$, then the area can be found as,
$\begin{align}
  & \,\,\,\,Area=\pi {{r}^{2}} \\
 & \,\Rightarrow \pi {{r}^{2}}=2\pi \\
 & \,\,\,\,\Rightarrow {{r}^{2}}=2 \\
\end{align}$
Using a calculator, or by finding it manually, we can find the radius up to a certain decimal. Ignore the negative values while finding the square root.
$\begin{align}
  & \Rightarrow r=\sqrt{2} \\
 & \Rightarrow r=1.414\,in \\
\end{align}$
Hence the radius is found to be 1.414 inches for this example. Therefore, we cannot expect only perfect squares as the area and sometimes we obtain decimal numbers as shown.