Question

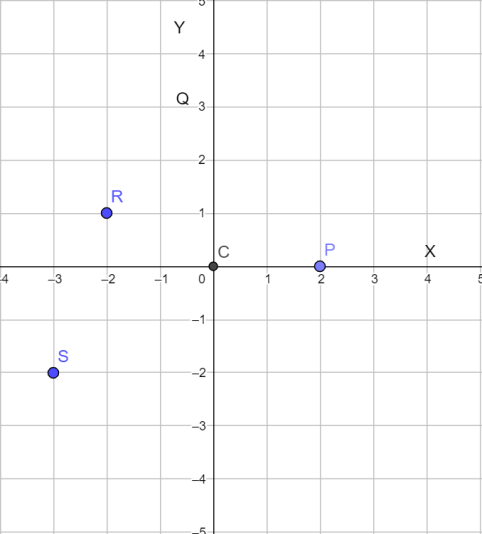
What are the coordinates of \[S\]?

\[\begin{align}
  & A.\left( 3,2 \right) \\
 & B.\left( 3,-2 \right) \\
 & C.\left( -2,3 \right) \\
 & D.\left( -3,-2 \right) \\
\end{align}\]

Answer 1

Hint: We are given with the points plotted on the graph. In order to find the coordinates of the particular point, we have to check the x-coordinate as well as the y-coordinate. These values give us the coordinates of the required point.

Complete step by step answer:
Now let us learn about the coordinates of a point. A coordinate of a point is nothing but the signed distance from the origin. The coordinates of a point are real numbers. Generally, the coordinates of an appointment define the position of the point on a \[2-D\]plane. There are two types of coordinates. They are: vertical coordinate and the horizontal coordinate. The most common coordinate system we use is the Cartesian coordinate system. With the help of the coordinate values, we can plot any point we point we desire upon a graph.
Now let us find out the coordinates of \[S\].
Firstly, we have to check the distance to \[S\] from the origin in both the ways i.e. both horizontally as well as vertically.
The distance from origin to \[S\] horizontally is \[3\]units. Since it is v units left to the origin the distance would be calculated with the negative sign.
\[\therefore \] The x-coordinate is \[-3\].
Now let us check the distance from origin to point \[S\] vertically.
We can see that it is \[2\] units downwards from the origin. Since it is \[2\] units downwards, it would be considered as negative.
\[\therefore \] The y-coordinate of point \[S\] is \[-2\].
Hence we can conclude the coordinates of point \[S\] as \[\left( -3,-2 \right)\].

So, the correct answer is “Option D”.

Note: We must be careful while assigning the signs to the coordinates of the point. We know that there exist four quadrants. We must have a note of the following points i.e. the coordinates are positive in the first quadrant. In the second quadrant, the x-coordinates are negative and the y-coordinates are positive. In the third quadrant, both the coordinates are negative. In the fourth quadrant, the x-coordinates are positive and the y-coordinates are negative.