Question

What are some examples of unbounded functions?

Answer 1

Hint: Here, first we will understand the meaning of bounded and unbounded functions. Now, to find the examples of these functions check if the value of the function does not go below or exceed above some particular real values. If there exist some particular values then that will be an example of a bounded function and if there does not exist any such particular value then that will be an example of an unbounded function.

Complete step-by-step solution:
Here we have been asked to write some examples of unbounded functions. First we need to know about bounded and unbounded functions.
In mathematics, a function $f\left( x \right)$ is said to be a bounded function if there exist some real value K such that $\left| f\left( x \right) \right|\le K$ for all real values of x on which the function is defined. It may be possible that there are two real values P and Q such that $P\le \left| f\left( x \right) \right|\le Q$. Here, P is called the lower bound of the function and Q is called the upper bound of the function. The mathematical inequality is stated as $f\left( x \right)$ is bounded below by Q and bounded above by P. A real valued function is bounded if and only if it is bounded from above and below. For example: - $\sin x$ is a bounded function because $-1\le \sin x\le 1$ and similarly $\cos x$ is also a bounded function. Other examples of bounded function are: - $\dfrac{1}{{{x}^{2}}+1}$, ${{\tan }^{-1}}x$ etc. Let us see the graph of some bounded functions from the above examples.

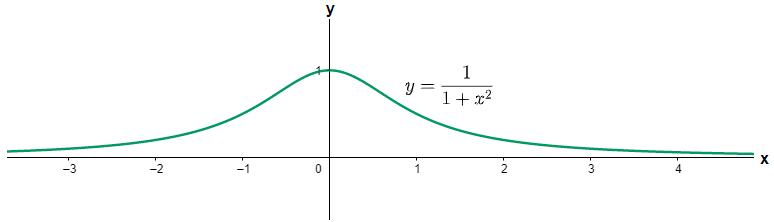
Here the range of the function $\dfrac{1}{{{x}^{2}}+1}$ is given as $\left( 0,1 \right]$.

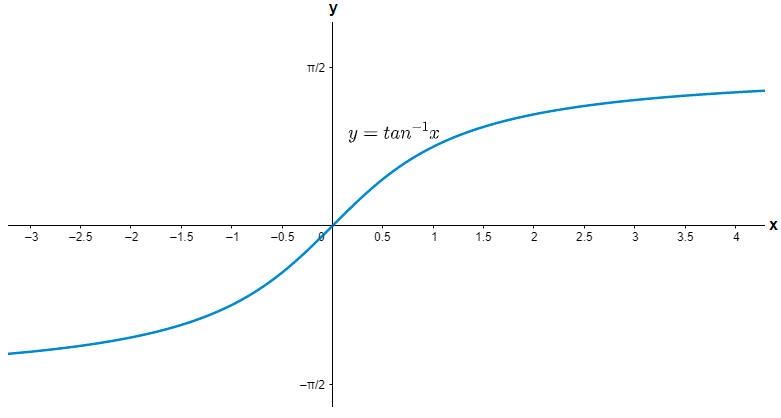
Here the range of the function ${{\tan }^{-1}}x$ is $\left( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right)$.
Now, a function which is not bounded from above or below by a finite limit is called an unbounded function. For example: - $x$ is an unbounded function as it extends from $-\infty $ to $\infty $. Similarly, $\tan x$ defined for all real x except for $x\in \left( 2n+1 \right)\dfrac{\pi }{2}$ is an unbounded function. Other examples of unbounded function can be: - $\dfrac{1}{x}$, $\dfrac{1}{{{x}^{2}}-1}$ etc. Let us see the graphs of some unbounded functions from the mentioned examples.

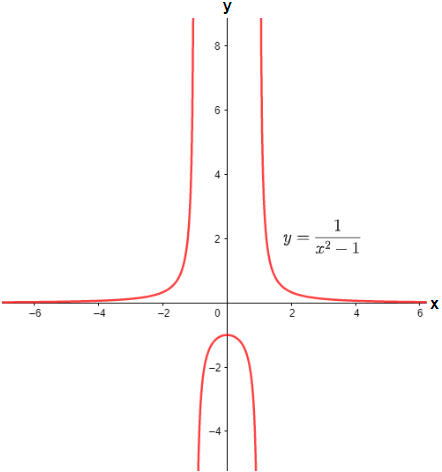
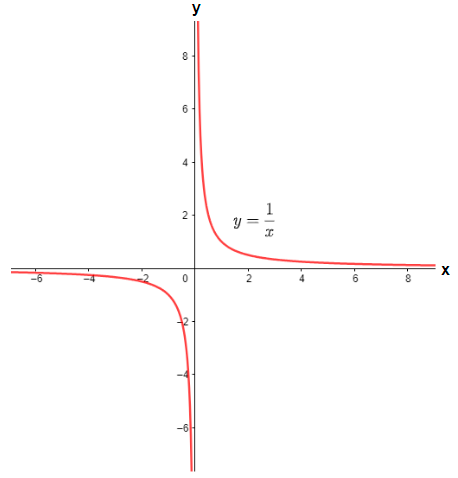
In the above two graphs we can see that the range of both the functions can be given as $\left( -\infty ,\infty \right)$.

Note: You can also understand the meaning of bounded and unbounded functions graphically. If we can draw two horizontal lines that define the upper and lower bound of a function, then that function can be called a bounded function. Now, if the graph of a function keeps on increasing or decreasing without any limit and we cannot draw any such two horizontal lines then that function will be called an unbounded function.