Question

How are ratio and proportion used in geometry?

Answer 1

Hint: From the question we are asked to explain the uses of the concept of ratio and proportion in geometry. Generally, we say in geometry using this concept of ratio and proportion that polygons are similar if the ratios of their sides are proportional. By using an example we will explain briefly the use of this concept in solving problems in geometry.

Complete step-by-step answer:
Firstly, the property which we use in geometry questions using the ratio and proportion concept is as follows.
If there are two or more than two polygons then they are said to be “similar” if the ratios of their sides are proportional.
We see this kind of thing when we zoom in or out. When we expand of shrink and when we work with scale drawings or maps.
For example, if a scale drawing has one side of a triangle is \[1\] inch and another is \[3\] inch, and the scale is \[1inch=1ft\], then in the built project, one side will be \[1ft\] and the other will be \[3ft\].
The ratio is still \[1:3\]

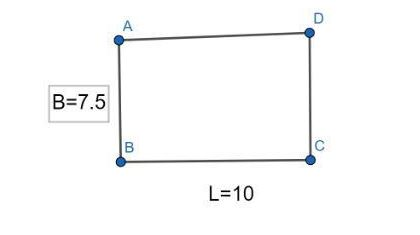
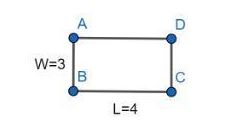
If we zoom in a rectangle with length \[4\] and width \[3\], then for any larger version there will be proportional sides.
So, if we make length \[10\], then we can find the width by solving the proportion;
\[\Rightarrow \dfrac{4}{3}=\dfrac{10}{w}\]
\[\Rightarrow 4w=30\]
\[\Rightarrow w=7.5\]
Therefore, in this way the ratio and proportion are used in geometry.

Note: Students should have a good conceptual knowledge ratio and proportions concept. Students must be able to interlink the concepts of geometry and ratio and proportion to solve questions of this theoretical type.
We can also explain using another example which is as follows. In any \[30,60,90\] triangle, the ratio of the hypotenuse and the short leg( opposite side of the angle) is the same. It is proportional.