Question

How are isosceles and equilateral triangles the same?

Answer 1

Hint: From the question we have been asked that how are the isosceles and equilateral triangles the same. For this question we will use the definition of the isosceles and equilateral triangle and explain the similarity among these both. So, we will proceed with the solution as follows.

Complete step-by-step answer:
We know that the isosceles triangles are the triangles where among the three sides two sides are equal in length and equilateral triangles are the triangles in which among the three sides all the three sides are equal in length.
So, from this definition of the isosceles and equilateral triangles we can say that these both triangles are not the same.
But, if we understand the definition of the triangles we explained in the above we can conclude that,
Any equilateral triangle (it has all \[3\] equal sides) is isosceles (that requires only \[2\] equal sides), but not all the isosceles triangles are equilateral.
For example, an equilateral triangle of side \[4\] can be an isosceles triangle with two sides as 4. But, an isosceles triangle with two sides as \[4\] cannot be an equilateral triangle with side as \[4\].

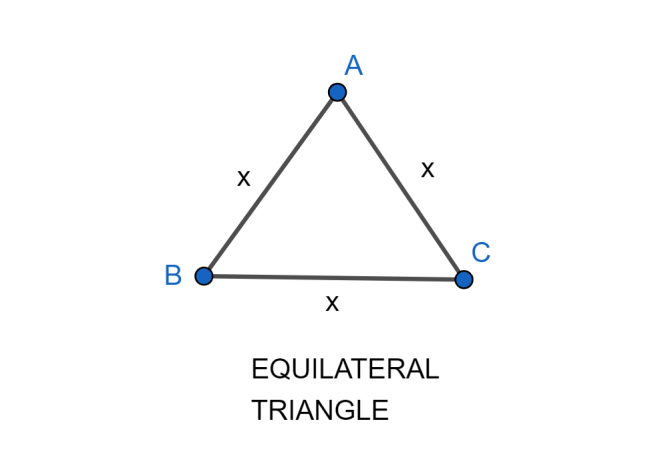
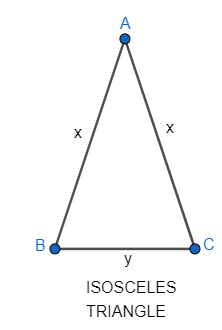
Therefore, this is the similarity between the isosceles and equilateral triangle.


Note: Students must have good knowledge in the concept of triangles and their properties. For solving these type of questions students must analyze the definitions very deeply. Students must be aware that “all equilateral can be isosceles but all isosceles need not be equilateral”.