Question

What are different types of graphs of quadratic function?

Answer 1

Hint: A quadratic function is a polynomial function with degree as \[2\] . The general form of quadratic polynomial is given by \[F(x) = a{x^2} + bx + c\] . The shape of the graph obtained from the general form of the quadratic function resembles the shape of Parabola . Parabola graphs can be of two types in which the parabola opens upwards and downwards with different conditions .

Complete step-by-step answer:
Given : \[F(x) = a{x^2} + bx + c\]
Where \[a\], \[b\] and \[c\] are variables such that \[a \ne 0\] .
The graph of the parabola can be upwards and downwards with conditions as follows :
If \[a < 0\] , then the graph will have the opening on the downward side .
If \[b < 0\] , then the graph will have the opening on the upward side .
Downward side graph can be represented as :

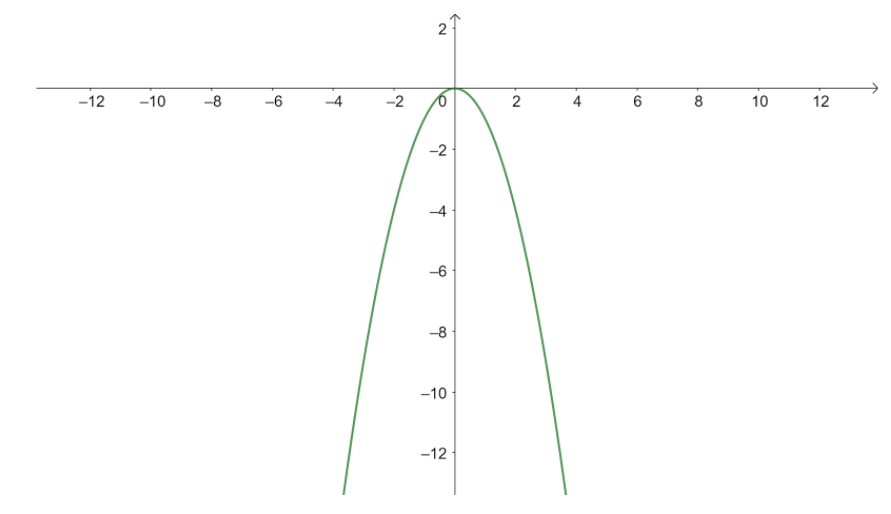
Upward side graph can be represented as :

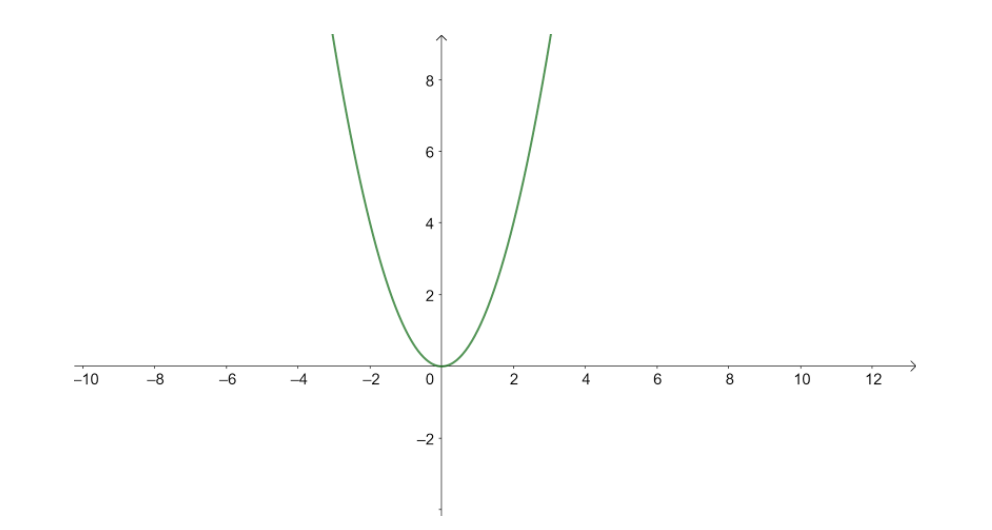
In both the graphs the origin is the vertex for both the parabolas and both the graphs have \[x - \] intercept at \[x = 0\] . The \[y - axis\] is acting as the axis of symmetry for both parabolas which divides them into two equal halves .

Note: Do not count the opening of the parabola horizontally . For example , If they have an opening about \[x - axis\] , it will be the same as the upwards and downwards count . For a given quadratic polynomial function the roots of the equation can be obtained from the graph at \[y = 0\] , which gives the value(s) of \[x\] . The vertex provides the maximum or minimum value for any parabola .