Question

Why are all equilateral triangles acute?

Answer 1

Hint: We know that, all equilateral triangles are all the three sides are equal. Angles are either right, which is to say \[{90^\circ }\] exactly, or obtuse, which is to say greater than \[{90^\circ }\] and less than \[{180^\circ }\], or acute, which is to say less than \[{90^\circ }\]. Also, acute angled triangles are the angles which are less than \[{90^\circ }\]. And, the sum of all the three angles of the triangles is \[{180^\circ }\]. Thus, by using this, we will get the final output.

Complete step-by-step answer:
We know that equilateral triangles have all three sides equal in length. Equal sides have equal angles at the opposite vertex.
Also, we know that an acute triangle is a triangle in which all of the measures of the angles of the triangle are less than \[{90^\circ }\]. We can determine if a given triangle is acute by determining the measures of its angles, and making sure they are all less than \[{90^\circ }\].
Thus, for a triangle to be equilateral, it must also have equal angles.
Since, each triangle has three angles and the sum of all the angles is equal to \[{180^\circ }\].
Let the angle of the triangle be x.
\[ \Rightarrow 3x = {180^\circ }\]
\[ \Rightarrow x = \dfrac{{{{180}^\circ }}}{3}\]
\[ \Rightarrow x = {60^\circ }\]
Thus, each interior angle is \[{60^\circ }\] which is less than \[{90^\circ }\].

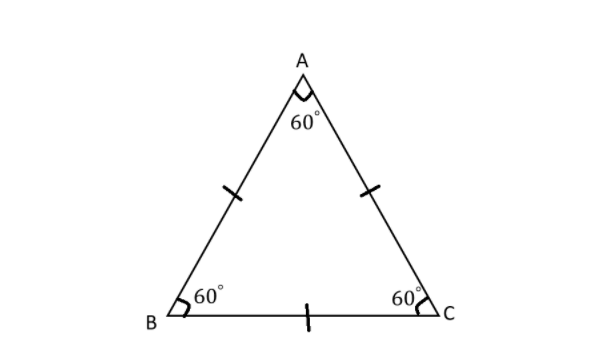
Let’s draw an equilateral triangle as below:
Here, length of AB = length of BC = length of AC.
Also, \[\angle A = \angle B = \angle C = {60^ \circ }\].
This means that all of the interior angles in it are acute. Equilateral triangles are always an acute triangle. An acute triangle is one in which all three angles are acute.
Thus, all equilateral triangles are acute but not all acute triangles are equilateral triangles.
Hence, equilateral triangles are all acute.

Note: An Isosceles has two equal sides (and more). It also has two equal angles (and more). All equilateral triangles are acute and isosceles. An equilateral triangle can never be obtuse. An equilateral triangle is therefore a special case of an isosceles triangle having not just two, but all three sides and angles equal. Another special case of an isosceles triangle is the isosceles right triangle.