
What is the approximate distance between the earth and moon?
A. 284400 Km
B. 384400 Km
C. 824400 Km
D. 124400 Km
Answer
586.8k+ views
Hint: Find the diameter of the moon and angle subtended on a person’s eyes when he tries to see two diametric end surfaces of moon. After that, use arc length formula for a sector of a circle given by:
$s = \theta \times r$
Where, s is arc length, θ is angle subtended by the sector in radians and r is radius of the sector.
Complete step by step answer:
The diameter of the moon is about 3,474.2 km long. When a person sees a full moon from earth, he will measure an angle of $0.56^\circ $subtending on his eyes.
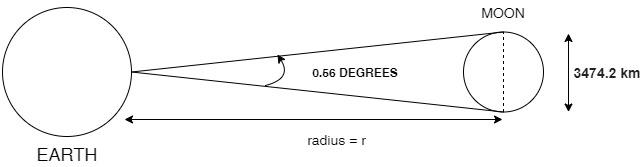
To find out how far away the moon is from the earth, let us consider a sector of a circle with earth at the center and the arc passing by the center of the moon, along one of its diameters. The moon is so far away that its straight diameter and slight curve of this arc are essentially the same things.
The arc that runs through the moon’s diameter has an angle of $0.56^\circ $and an arc length of 3,474.2 km (the diameter). Using the arc-length formula, solve for the radius of the sector, because this radius is the distance to the moon.
To solve for the radius:
The distance to the moon is
$r = \dfrac{{3474.2}}{{0.00977}} \approx 384400km$
So, the correct answer is “Option B”.
Note:
There are two ways in which we can measure the distance from the earth to the moon on our own: First using a Lunar eclipse and second using parallax method.
The Ancient Greeks used the Lunar eclipse method: Lunar eclipse is the phenomenon of the earth passing directly between the sun and the moon. To determine the distance from the Earth to its satellite moon . We do nothing but a simple tracking and calculating time, how long it takes the earth’s shadow to cross over the moon.
$s = \theta \times r$
Where, s is arc length, θ is angle subtended by the sector in radians and r is radius of the sector.
Complete step by step answer:
The diameter of the moon is about 3,474.2 km long. When a person sees a full moon from earth, he will measure an angle of $0.56^\circ $subtending on his eyes.

To find out how far away the moon is from the earth, let us consider a sector of a circle with earth at the center and the arc passing by the center of the moon, along one of its diameters. The moon is so far away that its straight diameter and slight curve of this arc are essentially the same things.
The arc that runs through the moon’s diameter has an angle of $0.56^\circ $and an arc length of 3,474.2 km (the diameter). Using the arc-length formula, solve for the radius of the sector, because this radius is the distance to the moon.
To solve for the radius:
- 1. First, let us change \[0.56^\circ \] to radians:
- 2. Input the values into the arc-length formula,
- 3. $ \Rightarrow 3,474.2\;km = {\text{ }}0.00977{\text{ }} \times \;r.$
- 4. Now, dividing each side by 0.00977.
$\begin{gathered}
\because 180{\text{ degrees = }}\pi {\text{ radians}} \\
\Rightarrow {\text{1 degree = }}\dfrac{\pi }{{180}}radians \\
\Rightarrow 0.56{\text{ degrees = }}\dfrac{{\pi \times 0.56}}{{180}}radians \\
{\text{ = 0}}{\text{.00977 radians}} \\
\end{gathered} $
$s = \theta \times r$
Where, s is arc length, θ is angle subtended by the sector in radians and r is radius of the sector.
Enter 0.00977 radians for the radian measure and 3,474.2 km for the arc length
The distance to the moon is
$r = \dfrac{{3474.2}}{{0.00977}} \approx 384400km$
So, the correct answer is “Option B”.
Note:
There are two ways in which we can measure the distance from the earth to the moon on our own: First using a Lunar eclipse and second using parallax method.
The Ancient Greeks used the Lunar eclipse method: Lunar eclipse is the phenomenon of the earth passing directly between the sun and the moon. To determine the distance from the Earth to its satellite moon . We do nothing but a simple tracking and calculating time, how long it takes the earth’s shadow to cross over the moon.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




