Question

Any point on the circumference of a rigid body which is rolling without slipping undergoes:
1.A circular path.
2.An elliptic path.
3.A cycloid path.
4.A parabolic path.

Answer 1

Hint: Rolling motion is a type of motion which combines rotational and translational motion together. We see rolling motion in each day of our lives for example moving wheels on an automobile along a highway, airplane wheels landing on the runway, etc.

Complete answer:
Step 1:
To understand rolling without slipping. In the case of rolling without slipping there is a linear (proportional) relation with velocity and acceleration at the centre of a mass of a wheel. Since, the motion is also rotational there would be a relation between linear velocity and acceleration with the angular acceleration and velocity. To better understand the relation, see the image below:

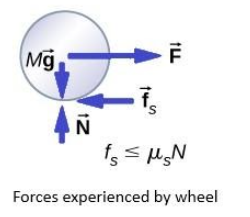
Here the force on the wheel is a linear force which is compensated by the frictional force, the natural weight of the ball (mg) which is applied on the ground is compensated by the Normal force (N) that the ground applies to the ball. The ball is at rest as all the forces cancel each other out.
Step 2: Find out the relation between the variables.

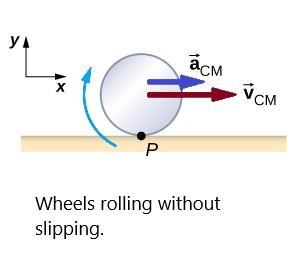
Here in the above diagram the wheel is rotating without slipping, so, there has to be a relation between the rotational motion and translational motion. It is given as:
$\omega $ = Angular Velocity
$v$= Linear Velocity
$R$= Radius
Similarly, Where:
$\alpha $= Angular Acceleration
= Linear Acceleration
$R$= Radius;
Since, the wheel has both the motions the total velocity of the wheel would be equal to the rotational velocity + Linear velocity.
${v_p} = - R\omega \widehat i + {v_{cm}}\widehat i$ … (The unit vector $\widehat i$ describes the direction in which the object is moving)
Since the ball is not slipping the velocity of the ball relative to the surface would be zero.
$0 = - R\omega \widehat i + {v_{cm}}\widehat i$
$ \Rightarrow R\omega = {v_{cm}}$
Now, we differentiate the L.H.S and R.H.S w.r.t time:
$\dfrac{{dR\omega }}{{dt}} = \dfrac{{d{v_{cm}}}}{{dt}}$
We know that the R is constant and acceleration is the rate of change of velocity w.r.t time $\dfrac{{d\omega }}{{dt}}$.
We can find out the relation between the angle and the distance covered:
${d_{cm}} = R\theta $

Option “3” is correct. Any point on the circumference of a rigid body which is rolling without slipping undergoes a cycloid path.

Note:
Here the answer seems to be circular path but it is not correct because a circular path is a helix motion meaning that the one component of the velocity is constant while in this case all the components of the velocity are changing that’s why it is a cycloid path.