Question

Anoop weights 48 kg, sits on a see-saw 4 m from the fulcrum. Another boy Ajay who weighs 64 kg wants to sit on the see-saw. What percent of the length away from the fulcrum, must he sit in order to balance Anoop?
(A) \[ - 20\% \]
(B) \[ - 25\% \]
(C) \[ - 15\% \]
(D) \[ - 10\% \]

Answer 1

Hint:Express the torque due to weight of Anoop and Ajay separately. Use the condition for equilibrium of the torque and determine the distance of Ajay from the fulcrum. To determine the percentage change in the length, take the ratio of difference in the distance of Ajay and Anoop to the distance of Ajay from the fulcrum.

Formula used:
The torque produced in the body due to the force F acting at a distance r from the fulcrum is,
\[\tau = Fr\sin \theta \]
Here, \[\theta \] is the angle between force and unit vector of distance.

Complete step by step answer:
We assume Ajay sits at a distance x m from the fulcrum so as to balance Anoop.

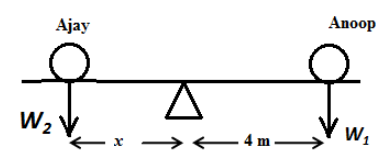
Now, we can express the torque produced due to weight of Anoop as follows,
\[{\tau _1} = {r_1}{W_1}\]
\[ \Rightarrow {\tau _1} = {r_1}{m_1}g\] …… (1)
Here, \[{r_1}\] is the distance of Anoop from the fulcrum, \[{W_1}\] is the weight Anoop, \[{m_1}\] is the mass of Anoop and g is the acceleration due to gravity.
Also, we can express the torque produced due to weight of Ajay as follows,
\[{\tau _2} = {r_2}{m_2}g\] …… (2)
Here, \[{r_2}\] is the distance of the Ajay from the fulcrum and \[{m_2}\] is the mass of Anoop.
We know that the system will be in the equilibrium if the net torque on the system is zero. We express the net torque on the system as follows,
\[{\tau _{net}} = {\tau _1} - {\tau _2} = 0\]
\[ \Rightarrow {\tau _1} = {\tau _2}\] …… (3)
From equations (1), (2) and (3), we have,
\[{r_1}{m_1}g = {r_2}{m_2}g\]
\[ \Rightarrow {r_1}{m_1} = {r_2}{m_2}\]
\[ \Rightarrow {r_2} = \dfrac{{{r_1}{m_1}}}{{{m_2}}}\]
Substituting 4 m for \[{r_1}\], 48 kg for \[{m_1}\] and 64 kg for \[{m_2}\] in the above equation, we get,
\[{r_2} = \dfrac{{\left( 4 \right)\left( {48} \right)}}{{64}}\]
\[ \therefore{r_2} = 3\,m\]
Therefore, we can calculate percentage change in the length away from the fulcrum as follows,\[\left( {\dfrac{{4 - 3}}{4} \times 100} \right) = 25\% \]

So, the correct answer is option (B).

Note: In equation (3), we have taken the torque due to the weight of Ajay in the direction opposite to the torque due to weight of Anoop. Therefore, \[{\tau _2}\] has negative signs. Although force and torque have the same physical meaning, the S.I unit of torque and force are different. The S.I unit of force is N while the S.I unit of torque is N m.