Question

What is the angle subtended by \[1m\] pole at a distance \[1km\] on the ground in sexagesimal measure?
(A) \[\dfrac{9}{50\pi }\]
(B) \[\dfrac{9}{5\pi }\]
(C) \[3.4\min \]
(D) \[3.5\min \]

Answer 1

Hint: We will first suppose that the angle subtended by the pole as \[\theta \]. The given description figures out a right angled triangle, which has the \[1m\] pole as the perpendicular and the \[1km\] on the ground as the base. We will now use the trigonometric function of tangent as only the perpendicular and base is given. Solving the expression gives the value of \[\theta \].

Complete step by step solution:
According to the given question, we have to find the angle subtended by the pole on the ground at a distance of \[1km\].
Sexagesimal measure refers to the use of minutes and seconds while describing or representing an angle which was previously described only using degrees.
Example - \[121.13{{5}^{\circ }}\sim {{121}^{\circ }}8'6''\]
In the question, we are given a pole which is \[1m\] long. The pole subtends an angle on the ground at a distance of \[1km\].
Let us suppose that the angle subtended by the pole on the ground be \[\theta \].
We have,

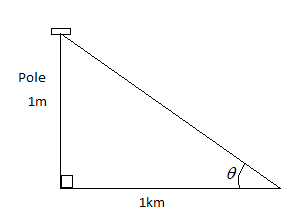
Since, we know the values of perpendicular and the base, so we can use the tangent function to find the angle subtended.
We have,
\[\tan \theta =\dfrac{1m}{1km}\]
As we know that, \[1km=1000m\]
So, we have,
\[\Rightarrow \tan \theta =\dfrac{1m}{1000m}=0.001\]
As we can see that the value of \[\tan \theta \] is very small, so we can assume that \[\tan \theta \] approximately as \[\theta \]
\[\theta ={{0.001}^{\circ }}\]
We can see there are no such answers in the options given.
We will convert it into radians and we get,
\[\Rightarrow \theta ={{0.001}^{\circ }}\times \dfrac{{{180}^{\circ }}}{\pi }\]
\[\Rightarrow \theta =\dfrac{1}{1000}\times \dfrac{180}{\pi }\]
\[\Rightarrow \theta =\dfrac{1}{100}\times \dfrac{18}{\pi }\]
\[\Rightarrow \theta =\dfrac{9}{50\pi }\]
Therefore, the angle subtended by a pole on the ground is (A) \[\dfrac{9}{50\pi }\].

So, the correct answer is “Option A”.

Note: Making the figure of the description as given in the question gives a clear sight of what to be found and also the ‘how’ as well. When we solved the trigonometric function, we got a value which was very small than 1. So we took \[\tan \theta \approx \theta ={{0.001}^{\circ }}\]. And the value of the angle we got was not in the options provided, so we converted it into the radians form. So, it is advisable to keep an eye on the options as well while solving the question and modify wherever required.