Question

Angle inscribed in a major segment is
(a) acute
(b) obtuse
(c) right
(d) straight

Answer 1

Hint: The definition of a segment in a circle is the portion of the circular region enclosed between a chord and the corresponding arc . The smaller portion is called the minor segment and the larger portion is called the major segment. We will sketch a rough diagram to visualize the major segment and the angle inscribed by it.

Complete step-by-step answer:
Let us draw a circle with centre O.

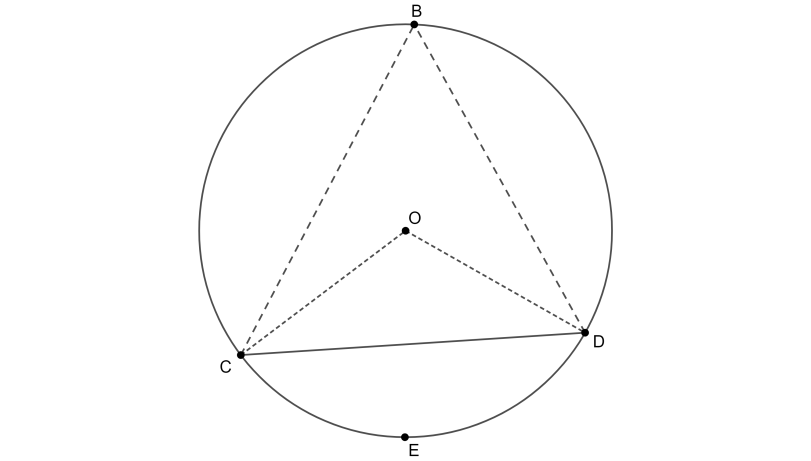
In this figure, segment CED is the minor segment and segment CBD is the major segment. The angle inscribed in the major segment is $\angle CBD$. We know that the inscribed angle is half of the central angle subtended by the same arc. We know that if the chord CD passes through the centre of the circle, then $\angle CBD=90{}^\circ $and therefore, the central angle is a straight line. The arc intercepted by $\angle CBD$ is arc CED. Now, in the figure above, $\angle COD<180{}^\circ $ and $\angle COD=2\angle CBD$.
Therefore, we get the relation $2\angle CBD<180{}^\circ $. Dividing both sides by 2, we get $\angle CBD<90{}^\circ $.
Therefore, the angle inscribed in the major segment is acute.

So, the correct answer is “Option A”.

Note: In this question, constructing a rough diagram is always helpful. After looking at the diagram, we can visualize the steps to prove a result. The same diagram will work if we have to find the angle inscribed by the minor segment. There is a possibility of confusion in the definition of a segment and a sector, so taking clues from the diagram is helpful.