Question

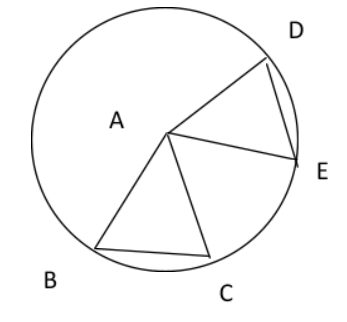
What is \[\angle DAE\]from the figure, \[BC = DE = 5\]and \[\angle BAC = {45^ \circ }\]?
A.\[{30^ \circ }\]
B.\[{45^ \circ }\]
C.\[{50^ \circ }\]
D.\[{60^ \circ }\]

Answer 1

Hint: Use the properties of triangle congruence to make the triangles congruent and hence use the properties after congruence with the help of the given angle to find our required angle. Triangle congruence will also help in finding other lengths.

Complete step by step answer:
We are given \[BC = DE = 5\]and \[\angle BAC = {45^ \circ }\],
We see here that the lengths \[AB = AD\]and \[AC = AE\]since they are the radii of the circle.
We are also given that the lengths BC and DE are equal.
That is the chord lengths of BC and DE are equal.
Thus it implies that the chords are congruent.
Hence, we have \[AB = AD\], \[AC = AE\]and \[BC = DE\]
We can note that all the sides of $\vartriangle BAC$ are equal to the corresponding three sides of the $\vartriangle DAE$. Hence $\vartriangle BAC$and $\vartriangle DAE$are congruent by SSS (Side-Side-Side) rule.
Hence by congruency, we get that the angles thus formed are also congruent.
So as we are given that \[\angle BAC = {45^ \circ }\]we find that the \[\angle DAE\]\[ = {45^ \circ }\]
Therefore, \[\angle DAE\]\[ = {45^ \circ }\].

Additional information:
Congruence in two or extra triangles depends on the measurements in their sides and angles. The 3 aspects of a triangle determine its size and the 3 angles of a triangle decide its shape. Two triangles are stated to be congruent if pairs in their corresponding aspects and their corresponding angles are identical. They are of identical form and size. There are many situations of congruence in triangles. Necessarily, now not all of the six corresponding factors of each of the triangles need to be observed to be the same to decide that they are congruent. Based on research and experiments, there are 5 conditions for two triangles to be congruent and they are SSS, SAS, ASA, AAS, and RHS congruence properties.

Note:
We must use the properties of triangles to use the congruency of triangles. Triangle congruency is important to find the unknown angles of triangles, lengths of triangles. It eases our calculation and helps us to get the desired solution.