Question

How many angle bisectors need to be drawn in the steps of construction of an angle \[45^\circ \]?
A) 0
B) 1
C) 2
D) 3

Answer 1

Hint:
Here, we will use the basic steps of construction to construct an \[45^\circ \] angle. We will calculate the number of angle bisectors used to construct it. Angle bisector is the line or line segment that divides an angle into two equal parts. So, we will construct an \[45^\circ \] angle using the compass and ruler and then see how many angle bisectors are used to construct an \[45^\circ \] angle.

Complete step by step solution:
To construct a \[45^\circ \] angle, firstly we need to construct perpendicular lines to obtain a \[90^\circ \] angle.
We will place a compass on an intersection point and adjust the compass to some width and make an arc on the base line and perpendicular line.
Now, with the help of the arc intersects base line and arc intersects perpendicular line we will make an angle bisector to construct an \[45^\circ \] angle.

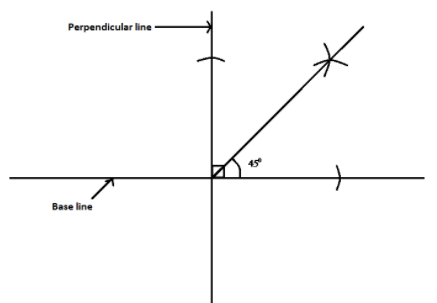
Here, we can see that only one angle bisector is used to construct an \[45^\circ \] angle.

Hence, option B is correct.

Note:
Geometry is the branch of mathematics that deals with points, lines and shapes. In geometry, bisection is said to be the division of something into two equal parts. Bisection is generally done with a line which is called a bisector. There are two main types of bisectors i.e. line segment bisector and angle bisector.
A line segment bisector is a line or line segment that divides the line into two equal parts or which passes through the midpoint of the line segment.
An angle has only one bisector. Also, there are two types of angle bisectors i.e. interior and exterior angle bisector.