Question

What is the angle between two vectors of equal magnitude when the magnitude of their sum is the same as the magnitude of each vector?
A.$120^\circ $
B. $240^\circ $
C. $90^\circ $
D. $30^\circ $

Answer 1

Hint: This question arises from motion in a plane (vectors). Here we apply the triangle law of vector addition. It states that if two vectors are represented both in magnitude and direction by the two sides of a triangle taken in the same order then the resultant of these vectors by the third side of the triangle taken in the opposite order.
That means ${\vec R = \vec A + \vec B}$

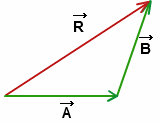
Complete step by step answer:
Let A and B be two vectors such that A=B. And the angle between two vectors A and B is$\alpha $. According to the question, the magnitude of the resultant vector R of vectors A and B is such that R=A=B.
Now according to the triangle law of vector addition, the magnitude of the resultant vector R
$R=[A^2+B^2+2ABcos \alpha]^{1/2}$
$ \Rightarrow {{\text{R}}^2} = {{\text{A}}^2} + {{\text{B}}^2} + 2{\text{ABcos}}\alpha $
$ \Rightarrow {{\text{A}}^2} = {{\text{A}}^2} + {{\text{A}}^2} + 2{\text{AAcos}}\alpha $
$ \Rightarrow 2{{\text{A}}^2} + 2{{\text{A}}^2}{\text{cos}}\alpha - {{\text{A}}^2} = 0$
$ \Rightarrow {{\text{A}}^2}(1 + 2{\text{cos}}\alpha {\text{) = 0}}$
$ \Rightarrow {\text{cos }}\alpha = \dfrac{{ - 1}}{2}$
$\therefore \alpha = {\text{arc cos}}\left( {\dfrac{{ - 1}}{2}} \right) = 120^\circ $

$\therefore$ The frictional force at the contact surface is ${m_1}\omega _1^2\,R$.
The maximum angular speed $\omega = \sqrt {\dfrac{{\mu _2^{}g}}{R}}$

Additional information:
The angle between two vectors of equal magnitude $0^\circ $, depending on the ratio of the magnitudes of the two vectors. Two vectors of equal magnitude that are pointing in opposite directions will sum to zero. Two vectors of unequal magnitude can never sum to zero.

Note:
When the vector quantities are given in magnitude they are represented in scalar form. Vector quantities cannot be added or subtracted algebraically. These quantities are specified by both magnitude and direction.