Question

An umbrella is made by stitching 10 triangular pieces of cloth of 5 different colours each piece measuring 20 cm, 50 cm and 50 cm. How many clothes of each colour is required for one umbrella?

Answer 1

Hint: In this question use the concept of Pythagoras theorem which says that hypotenuse square of a right triangle is equal to the sum of square of other two sides of a right angle triangle to use the Pythagoras theorem divide the triangular pieces into 2 equal right angle triangles also you can use the heron’s formula to find the area of the triangular piece use this information to get a better approach towards the solution.

Complete step-by-step answer:

According to the given information we have 10 triangular pieces of 2 different colors with sides which measures 20 cm, 50cm and 50 cm

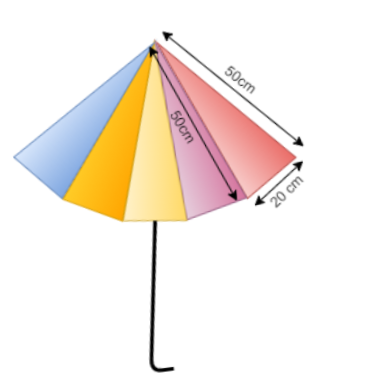
Since the triangular pieces have 2 equal opposite sides thus we can say that the 2 opposite angles are also equal to each other
Hence we can say that the triangular pieces showing the properties of isosceles triangle
Let’s divide the triangular pieces into 2 equal right angle triangles having equal bases and equal sides.

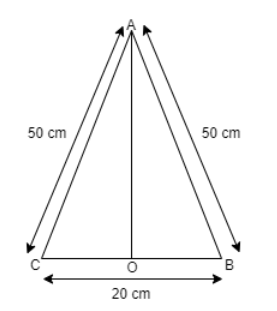
BC = 20 cm and OB = CO = ½ BC since triangle AOB and triangle AOC have equal bases
Therefore CO = OB = 10 cm
In triangle AOB by the Pythagoras theorem
$A{B^2} = A{O^2} + O{B^2}$ (Equation 1)
Substituting the values in equation 1
${\left( {50} \right)^2} = {\left( {AO} \right)^2} + {\left( {10} \right)^2}$
$ \Rightarrow $2500 = AO2 + 100
$ \Rightarrow $AO2 = 2500 – 100
$ \Rightarrow $$AO = \sqrt {2400} $
$ \Rightarrow $$AO = 20\sqrt 6 cm$
Now by the formula area of right angle triangle i.e. Area of triangle = $\dfrac{1}{2} \times base \times height$
Area of triangle AOB = $\dfrac{1}{2} \times OB \times AO$
$ \Rightarrow $Area of triangle AOB = $\dfrac{1}{2} \times 10 \times 20\sqrt 6 $
$ \Rightarrow $Area of triangle AOB = $100\sqrt 6 cm^2$
Area of triangle AOB and area of triangle AOC are equal to each other since triangle AOC and triangle AOB have equal base, height and hypotenuse
Since the area of triangular piece is equal to the sum of the area of triangle AOB and AOC
Therefore Area of triangle AOB = area of triangle AOC + area of triangle AOB
Since area of triangle AOC = Area of triangle AOB
Area of triangle ABC = 2 $ \times $Area of triangle AOB (equation 2)
Substituting the value of Area of triangle AOB in equation 2
Therefore Area of triangle ABC = 2 $ \times $$100\sqrt 6 $
$ \Rightarrow $ Area of triangle ABC = $200\sqrt 6 cm^2$
Since there are 5 different color and the umbrella have total 10 triangular pieces
Therefore each color have 2 pieces
So area of each color in umbrella = \[2 \times 200\sqrt 6 \]
$ \Rightarrow $ Area of each color = $400\sqrt 6 cm^2$
Hence cloth of each colour is required for one umbrella is $400\sqrt 6 cm^2$.

Note: We mentioned another way of solving this problem in the hint i.e. Heron’s formula so do you that the name of this concept was named after the hero of Alexandria this concept says that when the length of each side of a given triangle are identical then the concept of Heron’s formula is used to find the area of the given triangle. The area is calculated by the formula $A = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $ here s is the parameter of the given triangle and a, b and c are the sides of the triangle.