Question

An umbrella is made by stitching 10 pieces of cloth of two different colours, each piece measuring \[20cm,50cm,50cm\] . How much cloth of each colour is required for an umbrella?

Answer 1

Hint: We solve this problem by using the formula of area of triangle given as
\[A=\dfrac{1}{2}\left( \text{Base} \right)\left( \text{Height} \right)\]
Here, as all triangles are made of same dimensions we take one triangle and find the area. For finding the height of triangle we use the condition the height of isosceles triangle will be the median. By using the condition we find the height which gives the area.

Complete step by step answer:
We are given that the umbrella is made of 10 triangular pieces of two different colours.
Let us assume that the given two colours are green and white.
So, we can say that there are 5 triangular pieces of green colour and 5 pieces of white colour.
Let us take one triangle and draw the height as shown below.

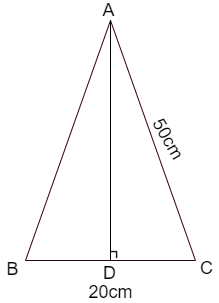
We are given that the dimensions of each triangle are \[20cm,50cm,50cm\]
So, from the triangle \[\Delta ABC\] we have
\[\begin{align}
  & \Rightarrow AB=AC=50cm \\
 & \Rightarrow BC=20cm \\
\end{align}\]
We know that the altitude of isosceles triangle will be the median
So, the point ‘D’ is mid – point of ‘BC’
So, we can the length of ‘DC’ as
\[\begin{align}
  & \Rightarrow DC=\dfrac{BC}{2} \\
 & \Rightarrow DC=\dfrac{20cm}{2}=10cm \\
\end{align}\]
We know that the Pythagoras theorem states that the square of hypotenuse is equal to sum of squares of other two sides that is for the triangle shown below

The Pythagoras theorem is given as \[{{b}^{2}}={{a}^{2}}+{{c}^{2}}\].
By using the above theorem to triangle \[\Delta ADC\] we get
\[\Rightarrow A{{D}^{2}}+D{{C}^{2}}=A{{C}^{2}}\]

Now by substituting the required values in above equation we get
\[\begin{align}
  & \Rightarrow A{{D}^{2}}+{{10}^{2}}={{50}^{2}} \\
 & \Rightarrow A{{D}^{2}}=2500-100 \\
 & \Rightarrow AD=\sqrt{2400}=20\sqrt{6}cm \\
\end{align}\]
Now, we know that the area formula of triangle is given as
\[A=\dfrac{1}{2}\left( \text{Base} \right)\left( \text{Height} \right)\]
Let us assume that the area of triangle \[\Delta ABC\] as \['a'\]
Then by using the area formula we get
\[\Rightarrow a=\dfrac{1}{2}\left( BC \right)\left( DC \right)\]
Now, by substituting the required values in above equation we get’
\[\begin{align}
  & \Rightarrow a=\dfrac{1}{2}\left( 20cm \right)\left( 20\sqrt{6}cm \right) \\
 & \Rightarrow a=200\sqrt{6}c{{m}^{2}} \\
\end{align}\]
We are given that there are 5 triangular pieces of each colour.
So, the total cloth of each colour is obtained by multiplying the area of each triangle by 5
Let us assume that the cloth required for each colour as \['A'\] then we get
\[\begin{align}
  & \Rightarrow A=a\times 5 \\
 & \Rightarrow A=200\sqrt{6}\times 5 \\
 & \Rightarrow A=1000\sqrt{6} \\
\end{align}\]

Therefore it requires \[1000\sqrt{6}c{{m}^{2}}\] of cloth of each colour is required for the given umbrella.

Note: Students may make mistakes in finding the answer.
We are given that there are 5 triangular pieces of each colour and asked to find the amount of cloth required for each colour then we need to multiply the area of each triangle by 5 not by 10.
So, we have the answer as
\[\Rightarrow A=a\times 5\]
But students do mistake and take the answer which is wrong as
\[\Rightarrow A=a\times 10\]