Question

An umbrella has 8 ribs, which are equally spaced. Assuming the umbrella to be a flat circle of radius 56 cm. Find the area between the two consecutive ribs.

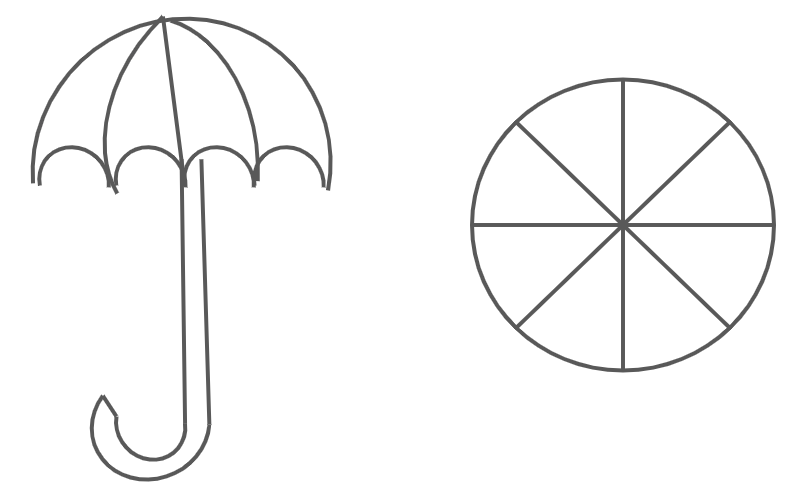
Answer 1

Hint: Here, we will first use the area of rib is calculated by using the formula, \[\dfrac{1}{8} \times {\text{Area of Umbrella}}\], where area of umbrella is same as the area of circle. Then we will use the formula of the area of the circle, \[\pi {r^2}\], where \[r\] is the radius of the circle to find the area of the umbrella.

Complete step-by-step answer:
We are given that the radius of the circle is 56 cm.
We know that the area of the rib is calculated by using the formula, \[\dfrac{1}{8} \times {\text{Area of Umbrella}}\], where the area of umbrella is same as the area of circle.
Using the formula of area of circle, \[\pi {r^2}\], where \[r\] is the radius of circle to find the area of umbrella, we get
\[
   \Rightarrow {\text{Area of umbrella}} = \pi {\left( {45} \right)^2} \\
   \Rightarrow {\text{Area of umbrella}} = \pi \times 2055 \\
 \]
Substituting the value of \[\pi \] in the above equation, we get
\[
   \Rightarrow {\text{Area of umbrella}} = \dfrac{{22}}{7} \times 2055 \\
   \Rightarrow {\text{Area of umbrella}} = \dfrac{{48510}}{7} \\
 \]

Substituting the value of area of umbrella in the formula of area of rib, we get
\[
   \Rightarrow {\text{Area of rib}} = \dfrac{1}{8} \times \dfrac{{48510}}{7} \\
   \Rightarrow {\text{Area of rib}} = \dfrac{1}{4} \times \dfrac{{22275}}{7} \\
   \Rightarrow {\text{Area of rib}} = \dfrac{{22275}}{{28}}{\text{ c}}{{\text{m}}^2} \\
 \]
Hence, the area between two consecutive ribs is \[\dfrac{{22275}}{{28}}{\text{ c}}{{\text{m}}^2}\].


Note: Since we have seen that there are 4 ribs on one side, so the total of ribs on top of the umbrella is 8. Then we will apply the conditions of the question on that variable to find out the value of that variable to find the result. We know that the area of an umbrella is the same as the area of a circle. Do not forget to write the units in the final answer.