Question

An orbiting satellite will escape if
A. Its speed is increased by $41\% $
B. Its speed in the orbit is made $\sqrt {1.5} $ times of its initial value
C. Its KE is doubled
D. It stops moving in the orbit

Answer 1

Hint: Firstly, we need to define the orbital velocity and escape velocity of Earth. From these, we can interpret the increase in the speed of the orbital velocity. The kinetic energy is directly proportional to velocity squared. From this, we can know the change in the kinetic energy of the satellite.
Formula used:
${V_{orbital}} = \sqrt {\dfrac{{GM}}{{R + h}}} $
${V_{escape}} = \sqrt {\dfrac{{2GM}}{R}} $
$K.E. = \dfrac{1}{2}m{v^2}$

Complete answer:
The orbiting satellite moves around the earth with a velocity called Orbital velocity. It is the velocity with which the satellites revolve around the earth, as shown in the figure.

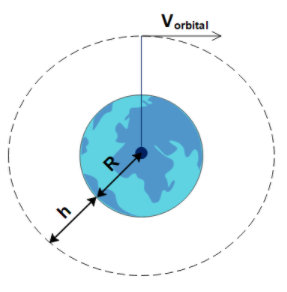
Orbital velocity is mathematically given by
${V_{orbital}} = \sqrt {\dfrac{{GM}}{{R + h}}} $
Where,
$G$ is the universal gravitational constant
$M$ is the mass of the Earth
$R$ is the radius of the Earth
$h$ is the height of the satellite from the Earth’s surface
Keeping this aside, the escape velocity of the Earth is the minimum velocity needed by any object to escape the Earth’s gravitational field.

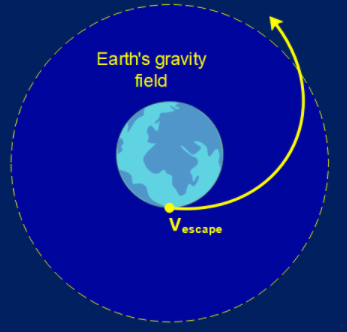
Escape velocity is mathematically given by
${V_{escape}} = \sqrt {\dfrac{{2GM}}{R}} $
An orbiting satellite must reach this velocity to escape Earth’s gravity. Thus, it must increase by $\sqrt 2 $ times its initial value. Then the percentage increase in the satellite’s velocity will be
$\eqalign{
  & \dfrac{{{V_{escape}} - {V_{orbital}}}}{{{V_{orbital}}}} \times 100 \cr
  & = \dfrac{{{V_{escape}} - {V_{orbital}}}}{{{V_{orbital}}}} \times 100 \cr
  & = \dfrac{{\sqrt 2 {V_{orbital}} - {V_{orbital}}}}{{{V_{orbital}}}} \times 100 \cr
  & = \dfrac{{\sqrt 2 - 1}}{1} \times 100 \cr
  & = 41\% \cr} $
Therefore, the speed increases by 41%.
As the velocity increased by $\sqrt 2 $,
The kinetic energy for any object can be given by
$K.E. = \dfrac{1}{2}m{v^2}$
From this, we have the relation, $K.E. \propto {v^2}$. Using this relation,
$\eqalign{
  & \dfrac{{{{\left( {K.E.} \right)}_{initial}}}}{{{{\left( {K.E.} \right)}_{final}}}} = {\left( {\dfrac{{{v_{initial}}}}{{{v_{final}}}}} \right)^2} \cr
  & \Rightarrow \dfrac{{{{\left( {K.E.} \right)}_{initial}}}}{{{{\left( {K.E.} \right)}_{final}}}} = {\left( {\dfrac{{{v_{initial}}}}{{\sqrt 2 \times {v_{initial}}}}} \right)^2} = \dfrac{1}{2} \cr
  & \Rightarrow {\left( {K.E.} \right)_{final}} = 2{\left( {K.E.} \right)_{initial}} \cr} $
Thus, the kinetic energy will be doubled.

Therefore, the correct option is A and C.

Note:
Any satellite will mostly keep rotating in the orbit, like the moon. In case, it stops moving the centripetal velocity will be lost and the satellite will give in to earth’s gravity. Thus, it will crash into Earth’s surface. The escape velocity and orbital velocity can also be written in the terms of acceleration due to gravity.