Question

An open vessel containing water is given a constant acceleration $a$ in the horizontal direction. Then the free surface of water get sloped with the horizontal at an angle $\theta $ given by:
$\left( A \right)\theta = {\tan ^{ - 1}}\left( {\dfrac{a}{g}} \right)$
$\left( B \right)\theta = {\tan ^{ - 1}}\left( {\dfrac{g}{a}} \right)$
$\left( C \right)\theta = {\sin ^{ - 1}}\left( {\dfrac{a}{g}} \right)$
$\left( D \right)\theta = {\cos ^{ - 1}}\left( {\dfrac{a}{g}} \right)$

Answer 1

Hint: First we will draw a rough diagram representing all the given parameters in the given problem. Then with the help of the diagram and the trigonometric formula we can find the angle $\theta $ which it makes with the free surface of water.


Complete step by step answer:
As per the given problem we have an open vessel containing water is given a constant acceleration $a$ in the horizontal direction and then the free surface of water gets sloped with the horizontal at an angle $\theta $.
We need to find the angle $\theta $ which has relation with acceleration of the water and acceleration due to gravity.

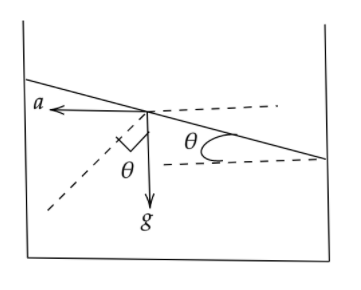
From the diagram we can see that there are two forces acting on the free surface of the liquid.
One is the force due to gravity or we can say weight of the liquid and the other is the force due to the acceleration of the water in the horizontal direction.
Now using trigonometric formula we can say that,
$\tan \theta = \dfrac{{{\text{perpendicular}}}}{{{\text{base}}}}$
Now from the figure the perpendicular force is due to horizontal acceleration and the bass force is due to gravity.
Hence,
$\tan \theta = \dfrac{{{\text{ma}}}}{{{\text{mg}}}}$
$ \Rightarrow \tan \theta = \dfrac{{\text{a}}}{{\text{g}}}$
Hence the angle will be,
$\theta = {\tan ^{ - 1}}\dfrac{{\text{a}}}{{\text{g}}}$
Therefore the correct option is (A).

Note: Remember that when a vessel moves under the action of acceleration then the liquid present in the vessel does not remain in the horizontal level it will move at an angle of $\theta $ in the horizontal direction. And the liquid will fall down in the direction of motion which rises up on one side of the water level.