Question

An open capillary tube contains a drop of water. When the tube is in its vertical position, the drop forms a column with a length of \[2{\text{ }}cm\]. The internal diameter of the capillary tube is \[1{\text{ }}mm\]. Determine the radii of curvature of the upper and lower meniscus in each case. Consider the wetting to be complete. Surface tension of water \[ = 0.0075{\text{ }}N/m\] .

Answer 1

Hint: We have a capillary tube in a vertical position. Using the internal diameter, we can find the pressure (${P_1}$). Using the hydrostatic pressure formula, we can find hydrostatic pressure(${P_2}$). After that, we can find the resultant pressure.

Complete step by step answer:
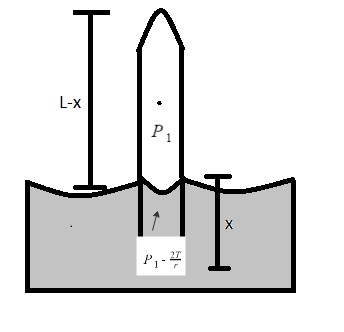
We know that when a capillary is in vertical position, then upper meniscus is concave and pressure (\[{P_S}\]) due to surface tension ($T$ ) is given as-
${P_S} = \dfrac{{2T}}{{{R_1}}}$
Where \[{P_S}\] is directed vertically upward and \[{R_1}\] being the radius of curvature of the upper meniscus.
Now, let \[r\] be the radius of the capillary tube and ${P_1}$ being the pressure when wetting is complete. So, the above equation becomes
${P_1} = \dfrac{{2T}}{r}$
As we know that \[r\] being the radius of the capillary tube.
Then \[r\] $ = \dfrac{D}{2} = \dfrac{1}{2}mm$
So, \[{R_1} = r = 0.5{\text{ }}mm\] in each case.
Now, after putting the values of $T = 75 \times {10^{ - 3}}N/m$ and $r = 0.5 \times {10^{ - 3}}m$, we have
$ {P_1} = \dfrac{{2T}}{r} $
$ \Rightarrow {P_1} = \dfrac{{2 \times 75 \times {{10}^{ - 3}}}}{{0.5 \times {{10}^{ - 3}}}} $
\[ \Rightarrow {P_1} = 300N/{m^2}\] ……………………... (i)
We know that the hydrostatic pressure \[{P_2} = h\rho g\]. ${P_2}$ is always directed downwards.
According to the question, the height of column $h = 2cm$. We know that the density of the water is ${10^3}kg/{m^3}$ and $g = 10m/s$.
So, putting the values in the equation, we get-
\[{P_2} = 2 \times {10^{ - 2}} \times 10 \times {10^3}\]
\[ \Rightarrow {P_2} = 200N/{m^2}\] ………………….. (ii)
It is clear from equation (i) and (ii) that \[{P_1} > {P_2}\].
So, it is clear that the resulting pressure is directed upward.
For equilibrium, the pressure due to the lower meniscus should be downward. This makes the lower meniscus concave downwards. Then the resultant pressure will be -
\[{P_1} - {P_2} = \dfrac{{2T}}{{{R_2}}}\]
\[ \Rightarrow 300 - 200 = \dfrac{{2 \times 75 \times {{10}^{ - 3}}}}{{{R_2}}}\]
$ \Rightarrow {R_2} = \dfrac{{2 \times 75 \times {{10}^{ - 3}}}}{{100}} $
$ \Rightarrow {R_2} = 1.50 \times {10^{ - 3}} $
$ \Rightarrow {R_2} = 1.50mm $

$\therefore$ The radii of the curvature are $1.50mm$.

Note:
In the above question, There are two types of pressures which can give us the resultant pressure. This resultant pressure gives the radii of curvature. We are required to find \[{P_1}\]which will be calculated for $r = 0.5mm$ This can be found by using the surface tension and pressure formula. The radius of the capillary must be used to find this pressure. To find \[{P_2}\]we have to use the height/length of the column $h = 2cm$. Both pressures will give the resultant pressure. Resultant pressure was obtained by their difference. We can use the formula ${P_1} - {P_2} = \dfrac{{2T}}{{{R_2}}}$ to find the resultant pressure. The direction of the resultant pressure is always the same as the direction of the pressure \[{P_1}\].