Question

An oil funnel of tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of a cone. If the total height be 22 cm, diameter of the cylindrical portion be 8 cm and the diameter of the top of the funnel be 18 cm, find the area of the tin required.

Answer 1

Hint: The curved surface area of the tin will be the area of the outer wall. In order to find the area first try to break the figure into parts. Consider the upper frustum and the below cylinder separately and finally sum them up.

Complete step-by-step answer:

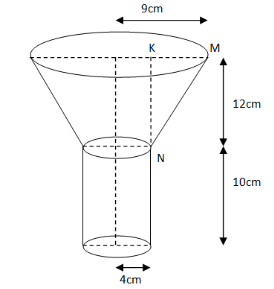
We will solve the problem with the help of the following figure. The following funnel consists of frustum at the top and the cylinder at the bottom.
Radius (R) of upper circular end of the frustum part $ = \dfrac{{18}}{2}cm = 9cm$
Radius (r) of lower circular end of the frustum part = Radius of circular end of cylindrical part $ = \dfrac{8}{2}cm = 4cm$
Height (h1) of the frustum part $ = 22 - 10 = 12cm$
Height (h2) of the cylindrical part $ = 10cm$
As we know that for any frustum with R and r as the bigger and smaller radius and h be its height
Slant height of the frustum is given by:
$l = \sqrt {{{\left( {R - r} \right)}^2} + {h^2}} $
So, the slant height of the following frustum is:
\[
   \Rightarrow l = \sqrt {{{\left( {R - r} \right)}^2} + h_1^2} \\
  l = \sqrt {{{\left( {9 - 4} \right)}^2} + {{12}^2}} \\
   = \sqrt {{5^2} + {{12}^2}} \\
   = \sqrt {25 + 144} \\
   = \sqrt {169} \\
   = 13cm \\
 \]
As we know the formula for CSA of cylinder and frustum
CSA of cylinder $ = 2\pi rh$
CSA of frustum $ = \pi \left( {R + r} \right)l$
From the above figure,
Area of the tin sheet required = Curved surface area of the frustum part + Curved surface area of the cylindrical part
$\therefore $ Area of tin sheet $ = \pi \left( {R + r} \right)l + 2\pi r{h_2}$
Substituting the values in the above equation we get:
$\therefore $ Area of tin sheet
\[
   = \pi \times \left( {9 + 4} \right) \times 13 + 2 \times \pi \times 4 \times 10 \\
   = \pi \times 13 \times 13 + 2 \times \pi \times 4 \times 10 \\
   = \pi \times 169 + \pi \times 80 \\
   = \pi \times 249 \\
   = 249 \times \dfrac{{22}}{7}{\text{ }}\left[ {\because \pi = \dfrac{{22}}{7}} \right] \\
   = 782.57143c{m^2} \\
 \]
Hence, the area of the tin required for the funnel \[ = 782.57143c{m^2}\]

Note: In order to find the area or the volume of some practical figures. It is important to recognize the geometrical shapes that comprise the figure. We need to break the figure in parts of known geometrical figures for easy calculation. Students must remember the formula for area of total surface, curved surface and the volume for some common geometrical figures.