Question

An observer of height 1.8 m is 13.2 m away from a palm tree. The angle of elevation of the top of a tree from his eyes is ${{45}^{\circ }}$. What is the height of the palm tree?

Answer 1

Hint: To solve this problem, first of all draw the diagram from the information given in the question. Now, let us assume that the height of the palm tree is “h”. As the observer and the palm tree are parallel to each other and as the height of the observer is definitely smaller than the palm tree so the height of the palm tree till the height of the observer is equal to 1.8 m and to find the remaining height of the palm tree subtract 1.8 m from “h”. Now, to find the remaining height of the palm tree apply the trigonometric ratio of $\tan {{45}^{\circ }}$ in triangle made from the angle of elevation of the observer, distance between observer and the tree and the remaining height of the tree.

Complete step-by-step answer:
In the below diagram, we have shown the height of the observer by AB, distance between observer and palm tree is shown by BD and AE and also shown the height of the palm tree by CD. We have also shown the angle of elevation by ${{45}^{\circ }}$.

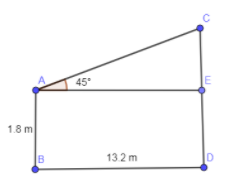
Let us assume that the height of the palm tree is “h”. Now, as you can see from the above diagram that $AB=ED$ so the length of ED is equal to 1.8 m.
From the above figure, you can also see that addition of sides CE and ED is equal to the height of the palm tree.
$CE+ED=CD$
We have assumed that height of the palm tree is “h” and also substituting ED as 1.8 m in the above equation we get,
$CE+1.8=h$
Subtracting both the sides by 1.8 we get,
$CE=h-1.8$……..Eq. (1)
Now, as you can see $\Delta CEA$ is a right angled triangle so applying trigonometric ratio of $\tan {{45}^{0}}$ we get,

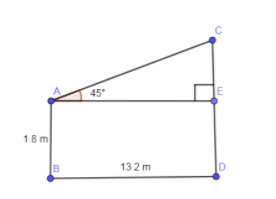
We know that,
$\tan {{45}^{\circ }}=\dfrac{P}{B}$
In the above equation, “P” stands for perpendicular corresponding to a given angle and “B” stands for the base corresponding to a given angle. Now, from the figure given above “P” is equal to CE and “B” is equal to AE.
$\tan {{45}^{0}}=\dfrac{CE}{AE}$
Substituting AE as 13.2 m and CE equal to h – 1.8 in the above equation we get,
$\tan {{45}^{\circ }}=\dfrac{h-1.8}{13.2}$
We know that the value of $\tan {{45}^{\circ }}=1$. Hence, substituting this value in the above equation we get,
$1=\dfrac{h-1.8}{13.2}$
On cross multiplying the above equation we get,
$\begin{align}
  & 13.2=h-1.8 \\
 & \Rightarrow 13.2+1.8=h \\
 & \Rightarrow 15m=h \\
\end{align}$
From the above solution, we have got the height of the palm tree as 15 m.

Note: The question demands knowledge of angle of elevation and the trigonometric ratio. Here you are lucky because the angle of elevation is ${{45}^{\circ }}$ even if you wrongly mark the angle of elevation the answer won’t change. For instance, in the below figure:

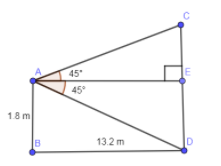
If you mark the angle of elevation as $\angle EAD$ then also you will get the right answer because when you do ${{90}^{\circ }}-{{45}^{\circ }}$ you will again get the angle ${{45}^{\circ }}$ which in turn will give you the right value of the height of the palm tree.