Question

An object with uniform density $\rho $ is attached to a spring that is known to stretch linearly with applied force as shown below.

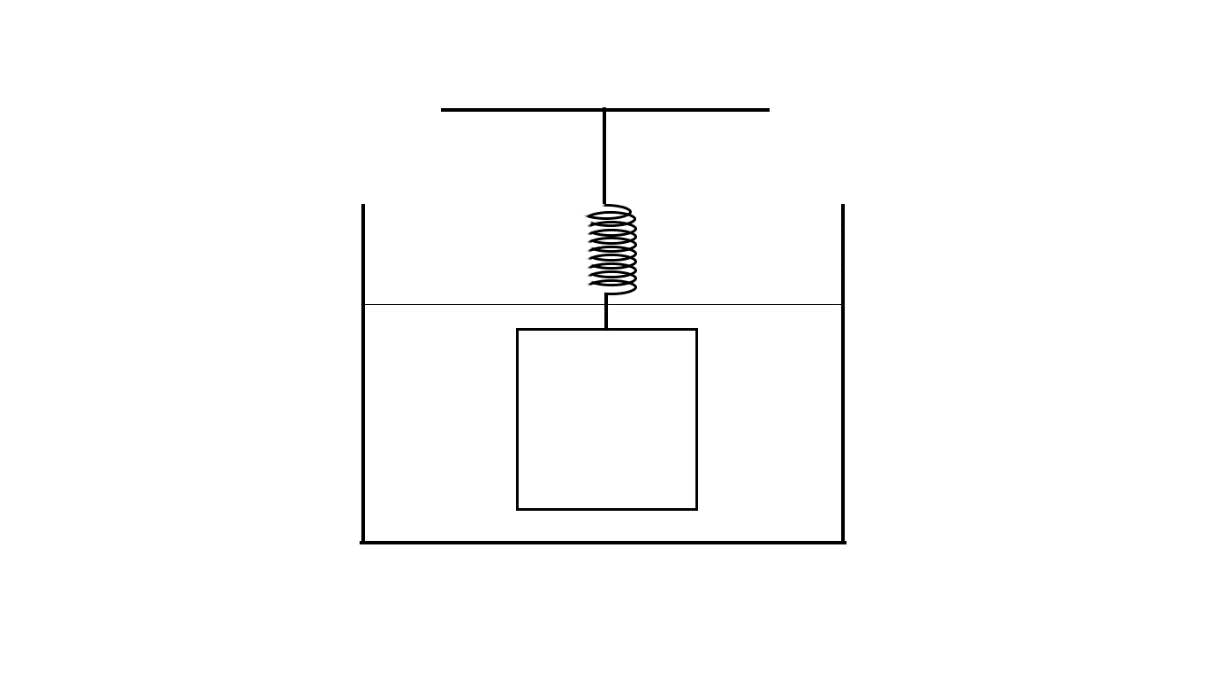
When the spring-object system is immersed in a liquid of density ${\rho _1}$ as shown in the figure, the spring stretches by an amount ${x_1}\left( {\rho > {\rho _1}} \right)$ . When the experiment is repeated in a liquid of density ${\rho _2} > {\rho _1}$ , the spring stretches by an amount ${x_2}$ . Neglecting any buoyant force on the spring, the density of the object is

Answer 1

Hint: In both the cases three forces act on the body, i.e. the downward force on the object due to its weight $ = mg = \rho vg$ (the density in this equation is the density of the object), the upwards pull on the object due to the spring $ = kx$ , and the upward buoyant force on the object $ = {\rho _1}vg$ (the density in this equation is the density of the liquid). The sum of all the three forces will be zero. You will get two separate equations for both the cases, subtract them from each other to calculate the value of $k$, and then the value of $\rho $ .

Complete answer:
When an object of a certain volume is immersed in a fluid, the object experiences an upward force equal to the weight of the fluid that was displaced by it, this is called the buoyant force.
Also, there is a spring attached to the top part of the object which will stretch due to the downward force on the object. The relation between the length by which the spring is stretched and the force applied on it is given by the equation
$F \propto x$
$F = kx$
Here, $k = $ Proportionality constant
There are two situations in the problem given to us.

For the first case, the object is submerged in the liquid of density ${\rho _1}$ .

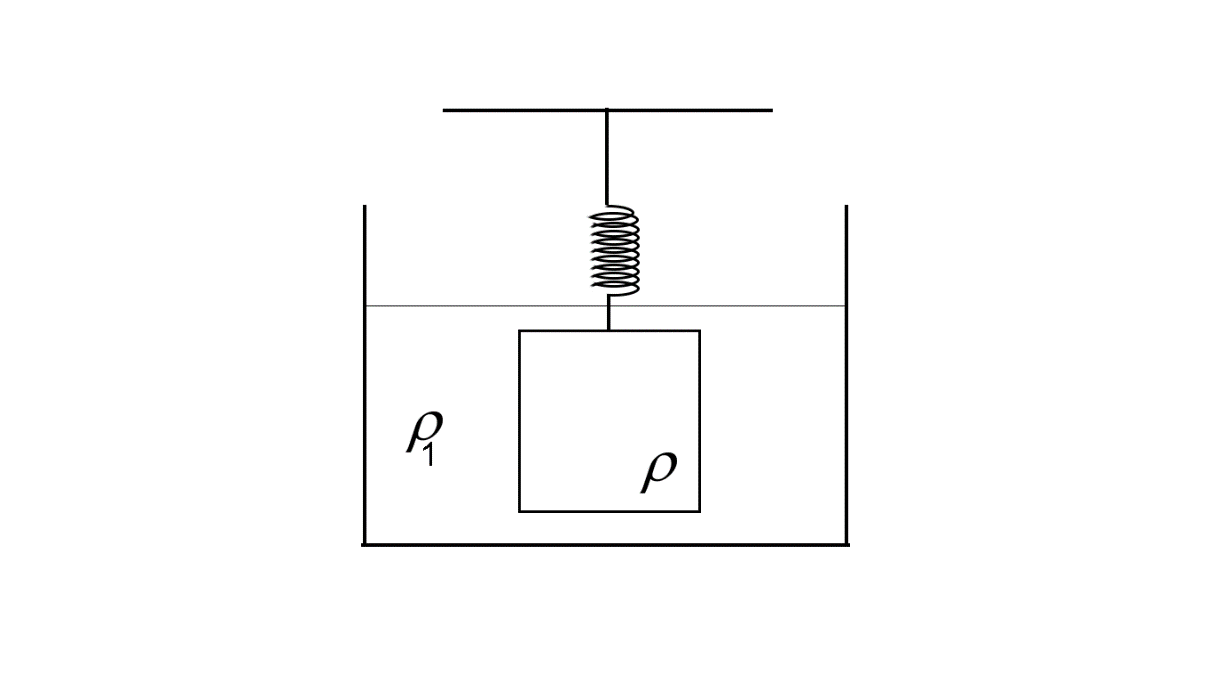
So the downward force on the object due to its weight $ = mg = \rho vg$ $\left( {\because \rho = \dfrac{m}{v}} \right)$
Here, $m = $ The mass of the object
$v = $ The volume of the object
$g = $ The acceleration due to gravity
$\rho = $ The density of the object
The upward buoyant force on the object $ = {\rho _1}vg$
The upwards pull on the object due to the spring $ = k{x_1}$
Since the position of the object does not change, the system is in equilibrium and the net force on the object is zero.
We also know that net force on the object $ = $ $\rho vg - {\rho _1}vg + k{x_1}$
So, $\rho vg - {\rho _1}vg + k{x_1} = 0$ (Equation 1)

For the second case, the object is submerged in the liquid of density ${\rho _2}$ .

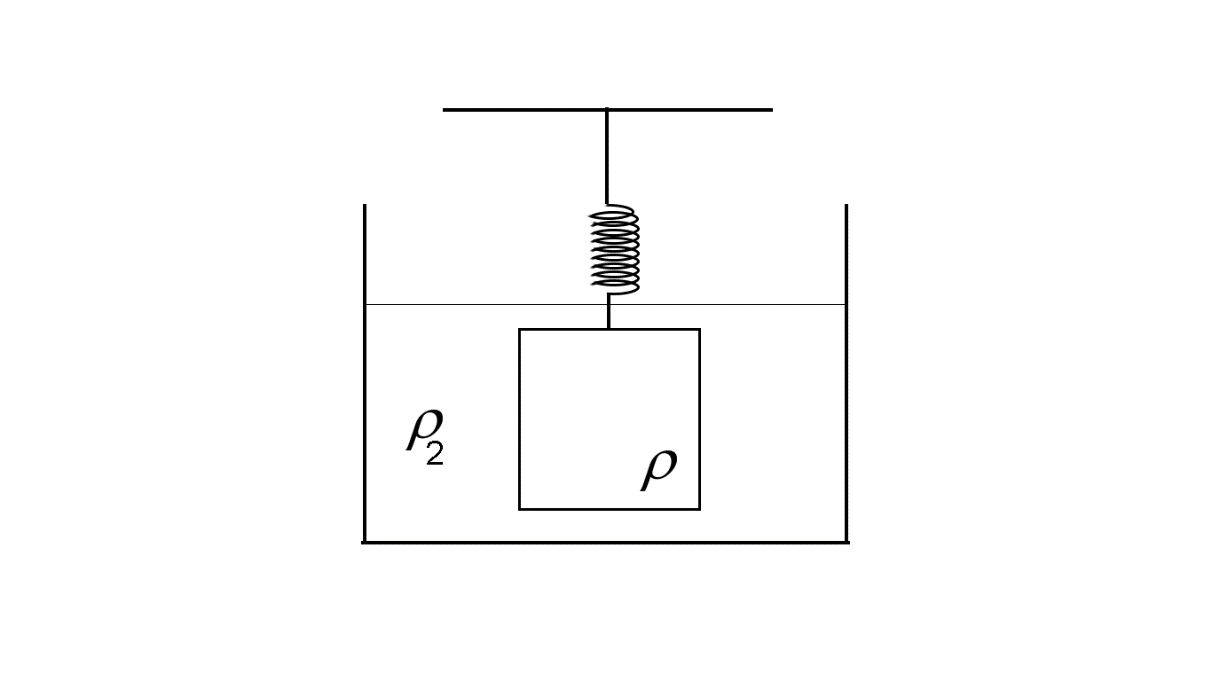
So the downward force on the object due to its weight $ = \rho vg$
The upward buoyant force on the object $ = {\rho _2}vg$
The upwards pull on the object due to the spring $ = k{x_2}$
Since the position of the object does not change, the system is in equilibrium and the net force on the object is zero.
We also know that net force on the object $ = $ $\rho vg - {\rho _2}vg + k{x_2}$
So, $\rho vg - {\rho _2}vg + k{x_2} = 0$ (Equation 2)
Subtracting equation 1 from equation 2, we get
$\rho vg - {\rho _1}vg + k{x_1} - \left( {\rho vg - {\rho _2}vg + k{x_2}} \right) = 0$
$k = \dfrac{{\left( {{\rho _2} - {\rho _1}} \right)vg}}{{\left( {{x_1} - {x_2}} \right)}}$
Substituting the value of $k$ in equation 1, we get
$\rho vg - {\rho _1}vg + \dfrac{{\left( {{\rho _2} - {\rho _1}} \right)vg}}{{\left( {{x_1} - {x_2}} \right)}}{x_1} = 0$
$\rho = \dfrac{{\left( {{\rho _2}{x_1} - {\rho _1}{x_2}} \right)}}{{{x_1} - {x_2}}}$
Hence, the density of the object is equal to $\dfrac{{\left( {{\rho _2}{x_1} - {\rho _1}{x_2}} \right)}}{{{x_1} - {x_2}}}$ .

Note:
In the solution above, while we were discussing the relationship between the force exerted on the spring (tension in the spring) and the extension of the spring, we discussed the equation $F = kx$ . $k$ in this equation is a proportionality constant that depends on the material used to make the spring. So springs made of different materials stretch to different lengths for the same applied force.