Question

An object starts sliding on a frictionless inclined plane and from the same height another object starts falling freely. Then
A. Both will reach the same speed.
B. Both will reach with the same acceleration.
C. Both will reach at the same time.
D. None of the above.

Answer 1

Hint: We will need to draw a diagram to understand the situation better. Then we will find the final velocities of two bodies by applying law of conservation of energy which states that energy can neither be created nor be destroyed, it can only be changed from one form to another. By finding the speed, acceleration, and time for the two cases, we will compare them and find out which of the given statements is correct.

Complete answer:
First, we will draw a detailed diagram of both cases in which the components of acceleration are clearly marked.


         

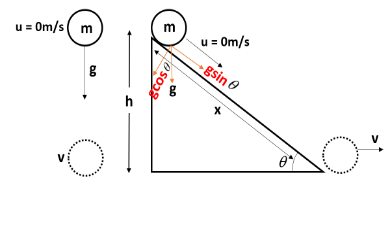
Here, the free falling body is having an acceleration $g$ downwards but the body sliding on the inclined plane only have the $\sin $ component of $g$, i.e. $g\sin \theta $ towards the direction of its motion.
So, we can cancel out the second option that both will reach the ground with the same acceleration.
Now, we will find the distance travelled by each body to reach the ground. The free falling body is travelling a distance of $h$ through its motion. But the body sliding on the inclined plane is travelling a distance of $x$ .

We can find $x$ using $\sin \theta $. $\sin \theta $ is given as the ratio of the opposite side of a triangle to its hypotenuse. I.e.

$\begin{align}
 & \sin \theta =\dfrac{\text{opposite}}{\text{hypotenuse}}=\dfrac{h}{x} \\
 & \Rightarrow x=\dfrac{h}{\sin \theta } \\
\end{align}$

But we know, $\sin \theta $ is always less than one. So we can say that $x>h$ . Hence, the sliding body is travelling more distance.

Here, both distances and accelerations of the bodies are different. So the time taken by both bodies to reach the ground will be also different. So we can cancel out the third option that both bodies will reach at the same time.
Now, we will apply the law of conservation of energy in both cases. Both the bodies are at rest and kept at a height $h$ . After their motion, both reach ground and the potential energy will be converted into kinetic energy. So according to law of conservation of energy,
$P.E=K.E$
If we look at the potential energies of each bodies,

$P.{{E}_{\text{sliding}}}=P.{{E}_{\text{free fall}}}=mgh$

As their potential energies are equal, according to the law of conservation of energy, their kinetic energies will be also equal. i.e.

$K.{{E}_{\text{sliding}}}=K.{{E}_{\text{free fall}}}=\dfrac{1}{2}m{{v}^{2}}$

Then their final velocities will be equal. That is ${{v}_{\text{sliding}}}={{v}_{\text{free fall}}}$ .
So, we can conclude that both bodies will reach the ground at the same speed. Therefore,

So, the correct answer is “Option A”.

Note:
We could easily find the answer to this problem without going through these many steps if we know this is an energy conservation based question. We must know that when a body is sliding on an inclined plane, only a part of acceleration due to gravity will be present towards its direction of motion.