Question

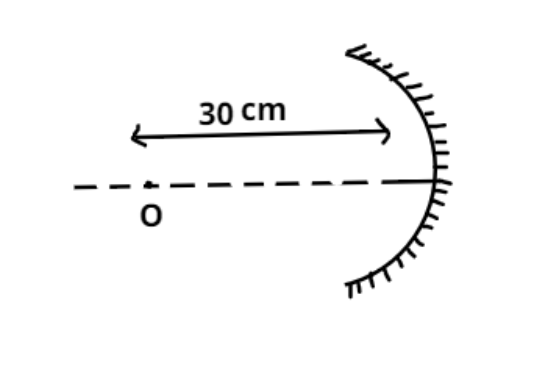
An object is present on the principal axis of a concave mirror at a distance 30 cm from it. Focal length of the mirror is 20cm. Image formed by mirror is:

(A). At a distance 60cm in front of mirror
(B). At a distance 60cm behind the mirror
(C). At a distance 12cm in front of mirror
(D). At a distance 12cm behind the mirror

Answer 1

- Hint: In this question use the direct relationship between image distance, object distance and the focal length that is $\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$, direct substitution of the values will help finding the image distance for the concave mirror.

Complete step-by-step solution -

Given data:
Object distance from the concave mirror is 30 cm.
Object distance is often denoted by u.
Therefore, u = -30 cm (‘-’ sign indicates in front of the mirror) as shown in the figure.
Now it is also given that the focus of the mirror is at 20 cm from the mirror.
Therefore, f = -20cm. (as focus is always in front of the mirror in case of a concave mirror, and ‘-’ sign indicates in front of the mirror).
Now let the image distance be at v cm from the mirror.
Now according to the mirror formula we have,
$\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$
Now substitute all the values in this equation we have,
$ \Rightarrow \dfrac{1}{v} + \dfrac{1}{{ - 30}} = \dfrac{1}{{ - 20}}$
Now simplify this we have,
$ \Rightarrow \dfrac{1}{v} = - \dfrac{1}{{20}} + \dfrac{1}{{30}}$
Now take L.C.M we have,
$ \Rightarrow \dfrac{1}{v} = \dfrac{{ - 30 + 20}}{{30\left( {20} \right)}}$
Now again simplify we have,
$ \Rightarrow \dfrac{1}{v} = \dfrac{{ - 10}}{{30\left( {20} \right)}} = - \dfrac{1}{{60}}$
Therefore, v = -60cm
So as we see that the distance comes out is negative so the image formed is in front of the mirror.
And the distance of the image is 60 cm from the mirror.
So this is the required answer.
Hence option (A) is the correct answer.

Note – The knowledge of the mirror formula is required for the solution. The trick here is only for the signs of the focal length and the object distance for the mirror. Distance lying towards the left of the mirror shall be taken as negative and towards the right side will be taken positive. Ignoring the signs may lead to incorrect answers.