Question

An object is observed from three points A, B and C in the same horizontal line passing through the base of the object. The angle of elevation at B is twice and at C thrice that of A. If AB = a, BC = b, then the height of the object is
a.\[\dfrac{a}{2b}\sqrt{\left( a+b \right)\left( 3b-a \right)}\]
b.\[\dfrac{a}{2b}\sqrt{\left( a-b \right)\left( 3b-a \right)}\]
c.\[\dfrac{a}{2b}\sqrt{\left( a-b \right)\left( 3b+a \right)}\]
d.\[\dfrac{a}{2b}\sqrt{\left( a+b \right)\left( 3b+a \right)}\]

Answer 1

Hint: Assume the angle of elevation at A be \[\alpha \] . The angle of elevation at B and will be \[2\alpha \] and \[3\alpha \] respectively. Now, find \[\angle PBA\] and \[\angle PCA\] using a linear pair of angles. As we know that the sum of all angles of a triangle is \[\pi \] , so using this find \[\angle BPA\] and \[\angle CPB\] . We will get BP=BA(sides opposite to equal angles are also equal). Now use the sine formula in the \[\Delta PCB\] and get the value of \[\sin \alpha \] . Using the identity, \[{{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1\] , get the value of \[\cos \alpha \] . We know that \[\sin 2\alpha =2\sin \alpha \cos \alpha \] . In \[\Delta PQB\] , apply \[\sin 2\alpha \] . Then, put the value of \[\sin \alpha \] , \[\cos \alpha \] , and BP=a. Solve further and get the value of PQ.

Complete step-by-step answer:

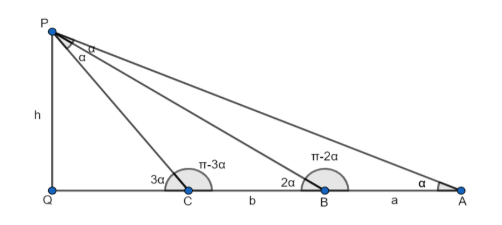
Let the angle of elevation at A be \[\alpha \] .
\[\angle PAQ=\alpha \] ……………………(1)
According to the question, it is given that the angle of elevation at B is twice and at C thrice that of A.
The angle of elevation at B that is \[\angle PBQ\] = \[2\alpha \] ………………….(2)
The angle of elevation at B that is \[\angle PCQ\] = \[3\alpha \] ………………………..(3)
\[\angle PBQ+\angle PBA=\pi \] (linear pair)
From equation (2), we can write \[\angle PBA=\pi -2\alpha \] ……………………………..(4)
Similarly, \[\angle PCQ+\angle PCA=\pi \] (linear pair)
From equation (3), we can write \[\angle PCA=\pi -3\alpha \] ……………………………..(5)
In \[\Delta PBA\] , we have
\[\angle BPA+\angle PAQ+\angle PBA=\pi \,(sum\text{ }of\text{ }all\text{ }angles\text{ }of\text{ }a\text{ }triangle\text{ }is\text{ }\pi )\] ………………………..(6)
Now, using equation (1) and equation (4), we can write equation (6) as,
\[\begin{align}
  & \angle BPA+\angle PAQ+\angle PBA=\pi \\
 & \Rightarrow \,\angle BPA+\alpha +\pi -2\alpha =\pi \\
 & \Rightarrow \angle BPA-\alpha =0 \\
\end{align}\]
\[\Rightarrow \angle BPA=\alpha \] ………………………….(7)
In \[\Delta PCB\] , we have
\[\angle PCB+\angle CPB+\angle PBC=\pi \,(sum\text{ }of\text{ }all\text{ }angles\text{ }of\text{ }a\text{ }triangle\text{ }is\text{ }\pi )\] ………………………..(8)
Now, using equation (2) and equation (5), we can write equation (8) as,
\[\begin{align}
  & \angle PCB+\angle CPB+\angle PBC=\pi \, \\
 & \Rightarrow \,\pi -3\alpha +\angle CPB+2\alpha =\pi \\
 & \Rightarrow \angle CPB-\alpha =0 \\
\end{align}\]
\[\Rightarrow \angle CPB=\alpha \] ………………………….(9)
We know the sine formula of a triangle.
We know the sine formula of a triangle, \[\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}\] .
Now, applying sine formula in the \[\Delta PCB\] ,
\[\dfrac{BC}{\sin \alpha }=\dfrac{PB}{\sin (\pi -3\alpha )}\]
We know the formula that, \[\sin 3\alpha =3\sin \alpha -4{{\sin }^{3}}\alpha \] and \[\sin \left( \pi -\theta \right)=\sin \theta \] . Using this formula, we get
\[\Rightarrow \dfrac{b}{\sin \alpha }=\dfrac{PB}{\sin 3\alpha }\]
\[\begin{align}
  & \Rightarrow \dfrac{b}{\sin \alpha }=\dfrac{PB}{3\sin \alpha -4{{\sin }^{3}}\alpha } \\
 & \Rightarrow b(3-4si{{n}^{2}}\alpha )=PB \\
\end{align}\]
We have, \[\angle BPA=\alpha \] and \[\angle PAB=\alpha \] .
So, PB = BA = a (sides opposite to equal angles are equal).
\[\begin{align}
  & \Rightarrow b(3-4si{{n}^{2}}\alpha )=a \\
 & \Rightarrow 3b-a=4b{{\sin }^{2}}\alpha \\
\end{align}\]
\[\Rightarrow \dfrac{\left( 3b-a \right)}{4b}={{\sin }^{2}}\alpha \]
\[\Rightarrow \sqrt{\dfrac{\left( 3b-a \right)}{4b}}=\sin \alpha \] ………………….(10)
We know the identity, \[{{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1\] . Now putting the value of \[\sin \alpha \] from equation (10) in the identity, we get
\[\begin{align}
  & \Rightarrow \dfrac{\left( 3b-a \right)}{4b}+{{\cos }^{2}}\alpha =1 \\
 & \Rightarrow {{\cos }^{2}}\alpha =1-\dfrac{\left( 3b-a \right)}{4b} \\
 & \Rightarrow {{\cos }^{2}}\alpha =\dfrac{4b-3b+a}{4b} \\
 & \Rightarrow {{\cos }^{2}}\alpha =\dfrac{a+b}{4b} \\
\end{align}\]
\[\Rightarrow \cos \alpha =\sqrt{\dfrac{a+b}{4b}}\] ………………………(11)
In \[\Delta PQB\] , we have
\[\dfrac{PQ}{BP}=\sin 2\alpha \]
\[\Rightarrow PQ=BP\sin 2\alpha \]
We have, \[\angle BPA=\alpha \] and \[\angle PAB=\alpha \] .
So, PB = BA = a (sides opposite to equal angles are equal).
\[\Rightarrow PQ=BA\sin 2\alpha \]
\[\Rightarrow PQ=a\sin 2\alpha \] ……………………(12)
We know the formula, \[\sin 2\alpha =2\sin \alpha \cos \alpha \] .
From equation (10), equation (11) and equation (12), we get
\[\begin{align}
  & \Rightarrow PQ=a.2\sin \alpha \cos \alpha \\
 & \Rightarrow PQ=a.2\sqrt{\dfrac{\left( 3b-a \right)}{4b}}\sqrt{\dfrac{a+b}{4b}} \\
 & \Rightarrow PQ=2a\dfrac{\sqrt{\left( 3b-a \right)\left( a+b \right)}}{4b} \\
 & \Rightarrow PQ=\dfrac{a}{2b}\sqrt{\left( 3b-a \right)\left( a+b \right)} \\
\end{align}\]
Hence, option (A) is the correct option.

Note: To solve this question, one may think to apply tan formulas in the \[\Delta PQC\] , \[\Delta PQB\] , and \[\Delta PQA\] . If we do so then we will get complex equations which will be difficult to solve. So, we don’t have to approach this question by applying a tan formula.