Question

An L-shaped object, made up of thin rods of uniform mass density, is suspended with a string as shown in figure. If $AB = BC$ , and the angle made by $AB$ with downward vertical is $\theta $ , then:

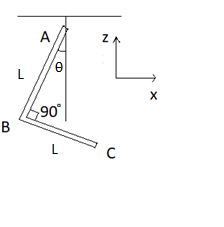
(A) $\tan \theta = \dfrac{2}{{\sqrt 3 }}$
(B) $\tan \theta = \dfrac{1}{3}$
(C) $\tan \theta = \dfrac{1}{2}$
(D) $\tan \theta = \dfrac{1}{{2\sqrt 3 }}$

Answer 1

Hint: to solve this problem we should know about the torque balancing:
Torque: it is the tendency of the body of a force to rotate a body to which it is applied.
Mathematically: $\tau = rF\sin \theta $ .
So to keep a body stable torque should be kept balanced.

Complete step by step solution:

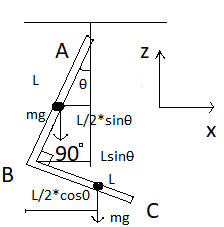
To solve this problem we have to balance torque experienced on two two limbs of the L-shape due to gravitational force.
So first take torque at first limb by gravitational force. By using figure we get,
 ${\tau _1} = mg\dfrac{L}{2}\sin \theta $
Same for the second limb torque due to gravitational force will be,
 ${\tau _2} = mg\left( {\dfrac{L}{2}\cos \theta - L\sin \theta } \right)$
To keep the torque balance at both points the direction will be reversed to each other.
So, In magnitude both will be equal.
 $ \Rightarrow mg\left( {\dfrac{L}{2} + L} \right)\sin \theta = mg\dfrac{L}{2}\cos \theta $
 $ \Rightarrow mg\dfrac{{3L}}{2}\sin \theta = mg\dfrac{L}{2}\cos \theta $
 $ \Rightarrow \tan \theta = \dfrac{1}{3}$
From above calculation. We get $\tan \theta = \dfrac{1}{3}$ .
So, option (b) is the correct option.

Note:
As all rotational motion have an axis of rotation, torque must be defined about a rotational axis. So, a torque is a force applied to a point on an object about the axis of rotation. Torque is an important part of generating power from a car’s engine and transmission of power. For a given force torque can be increased by increasing the radius about which it acts.