Question

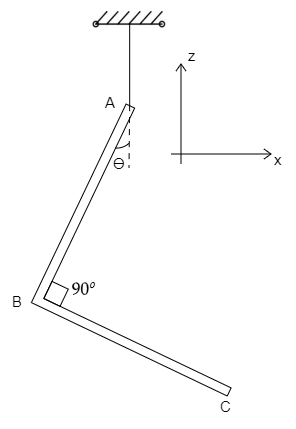
An L-shaped object, made of thin rods of uniform mass density, is suspended with a string as shown in figure. If $AB = BC$, and the angle made by $AB = B$, and the angle made by $AB$ with downward vertical is $\theta $, then

A. $\tan \;\theta = \dfrac{2}{{\sqrt 3 }}$
B. $\tan \;\theta = \dfrac{1}{3}$
C. $\tan \;\theta = \dfrac{1}{2}$
D. $\tan \;\theta = \dfrac{1}{{2\sqrt 3 }}$

Answer 1

Hint: Since, the object has uniform mass. Hence, the weight of the two-section is acted downwards. By calculating the moment at the point, A due to the weight of the rods. Then, the value of the $\tan \;\theta $ can be calculated. Also, the rod is in equilibrium, so the moment due to the two forces are equal.

Formula used:
Moment, $M = F \times d$
Where $F$ is the force and $d$ is the perpendicular distance.
In a right-angled triangle,
${\text{sin}}\theta {\text{ = }}\dfrac{{{\text{Opposite side}}}}{{{\text{Hypotenuse}}}}$
$\cos \theta {\text{ = }}\dfrac{{{\text{Adjacent side}}}}{{{\text{Hypotenuse}}}}$

Complete step by step answer:
The L-shaped rod is considered to be two parts as AB and BC, both have the same mass $m$ and P, Q are the center points of the rod BC and AB respectively.

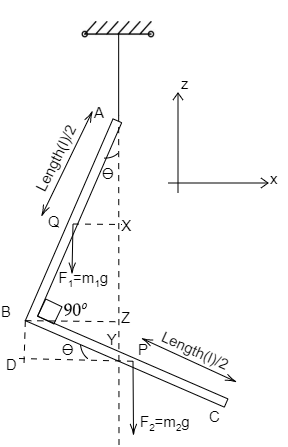
The rod is in equilibrium. Thus, the total moment at hanged point A is zero.
${M_1} + {M_2} = 0$
Where, ${M_1}$ is the moment due to the weight of the rod AB and ${M_2}$ is the moment due to the weight of the rod BC.
Since the moment ${M_2}$ is in a clockwise direction, so it is negative.
${M_1} + \left( { - {M_2}} \right) = 0$
$ \Rightarrow {M_1} = {M_2}$
By applying moment formula, we get
${F_1} \times QX = {F_2} \times PY\,.........................................\left( 1 \right)$
Where, ${F_1}$ is the force due to the self-weight of the rod AB, ${F_2}$ is the force due to the self-weight of the rod BC, $QX$ is the perpendicular distance between ${F_1}$ and the point A and $PY$ is the perpendicular distance between ${F_2}$ and the point A.
Since, $F = mg$
Where $m$ is the mass of the body and $g$ is the acceleration due to gravity.
Thus,
$ \Rightarrow {F_1} = {m_1}g$ and ${F_2} = {m_2}g$
Here, the rod AB and BC has the same mass. So, $m = {m_1} = {m_2}$ and also ${F_1} = {F_2} = F = mg$
By applying trigonometric function in the triangle AQX,
$\sin \theta = \dfrac{{QX}}{{AQ}} = \dfrac{{QX}}{{\left( {\dfrac{l}{2}} \right)}} \Rightarrow QX = \dfrac{l}{2} \times \sin \theta $
By applying trigonometric function in the triangle PBD,
$\cos \theta = \dfrac{{PD}}{{PB}} = \dfrac{{PD}}{{\left( {\dfrac{l}{2}} \right)}} \Rightarrow PD = \dfrac{l}{2} \times \cos \theta $
By applying trigonometric function in the triangle ABZ,
$\sin \theta = \dfrac{{BZ}}{{AB}} = \dfrac{{BZ}}{l} \Rightarrow BZ = l \times \sin \theta $
Since, $BZ = DY = l \times \sin \theta $
Thus, from the diagram, we get
$PY = PD - DY$
$ \Rightarrow PY = \left( {\dfrac{l}{2} \times \cos \theta } \right) - \left( {l \times \sin \theta } \right)$
By substituting the values of ${F_1}$, ${F_2}$, $QX$ and $PY$ in the equation (1), we get
$mg \times \left( {\dfrac{l}{2}\sin \;\theta } \right) = mg \times \left( {\dfrac{l}{2}\cos \;\theta - l\sin \;\theta } \right)$
By cancelling common terms on both sides,
$ \Rightarrow \left( {\dfrac{l}{2}\sin \;\theta } \right) = \left( {\dfrac{l}{2}\cos \;\theta - l\sin \;\theta } \right)$
By rearranging the sin terms to one side, we get
$ \Rightarrow \dfrac{l}{2}\sin \;\theta + l\sin \;\theta = \dfrac{l}{2}\cos \;\theta $
By performing arithmetic operation, we get
$ \Rightarrow \dfrac{{3l}}{2}\sin \;\theta = \dfrac{l}{2}\cos \;\theta $
Rearranging the terms, we get
$ \Rightarrow \dfrac{{\sin \;\theta }}{{\cos \;\theta }} = \dfrac{l}{2} \times \dfrac{2}{{3l}}$
Since, $\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}$
By substituting the above relation in the equation, we get
$\therefore \tan \;\theta = \dfrac{1}{3}$

Hence, the option (B) is correct.

Note:
The weight of the two rods tends the whole setup to be in equilibrium. The torque developed by the two rods is in the opposite direction. Thus, the Torque cancels each other to make the rod in equilibrium. If any additional force is applied to the rod, it experiences an additional torque. Then, the rod tends to move in any of the directions based on the direction of force applied.