Question

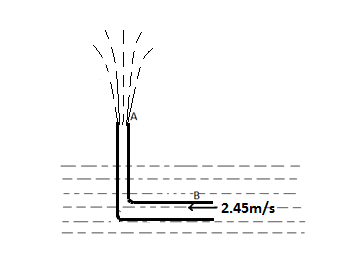
An L shaped tube with a small orifice is held in a water stream as shown in figure. The upper end of the tube is \[10.6cm\] above the surface of water. What will be the height of the jet of water coming from the orifice? (Velocity of water stream is \[2.45~m/s\])
 

A. \[Zero\]
B. \[20.0cm\]
C. \[10.6cm\]
D. \[40.0cm\]

Answer 1

Hint: Here, velocity of water stream and tube length is given. We can apply the continuity equation. The equation describes that in any steady state process, the rate at which mass leaves the system is equal to the rate at which mass enters a system.
Formula used:
\[{{A}_{1}}{{V}_{1}}={{A}_{2}}{{V}_{2}}\]
\[{{v}^{2}}={{u}^{2}}+2aS\]

Complete answer:
Applying continuity equation,
\[{{A}_{1}}{{V}_{1}}={{A}_{2}}{{V}_{2}}\]
Where \[{{A}_{1}}\]- Cross sectional area of tube at A
\[{{A}_{2}}\]- cross sectional area of tube at B
\[{{V}_{1}}\]- Velocity of water at A
\[{{V}_{2}}\]- Velocity of water at B

Here,
\[{{A}_{1}}={{A}_{2}}\]
Then,
\[{{V}_{1}}={{V}_{2}}\]
Here,
\[{{V}_{2}}=2.45\text{ m/s}\]
Since the other end of the tube is open, atmospheric pressure will be acting on water coming out of the tube.
To find the height of the jet of water coming from the orifice, apply equation of motion,
\[{{v}^{2}}={{u}^{2}}+2aS\]-------- 1
Here \[{{v}^{2}}\] is zero, as the water reaches its maximum height its velocity becomes zero.
\[{{u}^{2}}\]is the initial velocity which is \[{{V}_{2}}=2.45\text{ m/s}\]
and \[a\] is the acceleration due to gravity, \[a=10\text{ m/}{{\text{s}}^{2}}\]
Applying the above values in equation 1
We get,
\[0={{\left( 2.45 \right)}^{2}}+2\times 10\times S\]
Solving the equation we get,
\[S=30.6\text{ cm}\]
This height is achieved by a water jet from the upper end of the tube.
Here, it is given that the upper end of the tube is \[10.6cm\] above the water surface.
Then,
Height the jet of water coming from the orifice \[\text{=}30.6\text{ cm}-10.6\]=\[20\text{ cm}\]

So, the correct answer is “Option B”.

Note:
Continuity equation is another form of conservation of mass. It expresses the law of conservation of mass at each point in a fluid. Therefore it must be satisfied at every point in a flow field. It applies to all materials, not just fluids. Hence, it applies to solids as well.